| 5.0. Grundlagen der Logik - Bool'sche Aussagenlogik und de'Morgan'sche Theoreme |
|
|
Letztmalig dran rumgefummelt: 05.11.25 16:54:22 |
| Eine Hauptaufgabe der
mathematischen Logik ist die Untersuchung des formalen Denkens und
Schließens mit Hilfe mathematischer Methoden, die z. B. der Algebra und der
Algorithmentheorie entnommen sind. Diese ursprünglich aus der Philosophie stammende Aufgabe ist jedoch nicht ihre einzige; die mathematische Logik umfasst heute eine Vielzahl von Fragestellungen und Anwendungen auf den verschiedensten Gebieten, z. B. in den Naturwissenschaften, in der Schaltalgebra, in der Theorie informationsverarbeitender Systeme, in der Linguistik und in verschiedenen Disziplinen der Gesellschaftswissenschaften wie Philosophie, Rechtswissenschaft und Ethik. Entscheidende Impulse für die Entwicklung der mathematischen Logik ergaben sich aus der Situation der Mathematik am Ausgang des 19. Jahrhunderts. Diese hatte bis dahin eine Fülle einzelner Resultate gesammelt und schon einen hohen Abstraktionsgrad erreicht, ohne dass über den Inhalt der intuitiv verwendeten Grundbegriffe, z. B. des Mengenbegriffs und des logischen Schließens, ausreichende Klarheit bestand. Neben dem Bedürfnis nach einer zweifelsfreien Begründung des Mengenbegriffs ergab sich zum ersten Male die Notwendigkeit einer Einsicht in das, was Logik und logische Deduktion eigentlich bedeuten. |
|||||||||||||||||||||||||||||||||
| 0. Bool'sche Algebra und deren
technische Umsetzung 1. Klemmverhalten logischer Schaltungen 2. Allgemeines zur Logik und Kombinatorik 3. De Morgan'sche Theoreme 4. Schaltungslogik - Torschaltungen 5. Verwandte Themen 6. Übungsaufgaben |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| der Aufbau von logischen Schaltungen folgt der Bool'schen Algebra und kann nach den de Morgan'schen Theoremen verkürzt werden | |||||||||||||||||||||||||||||||||
| Eingänge von Logikschaltungen dürfen parallel geschalten werden, wobei lediglich die mögliche Stromabgabe der Quelle zu beachten ist - in der TTL-Technik spricht man von TTL-Lasten, wobei der typische Wert 10 ist (Leitungstreiber erreichen höhere Werte), d. h. an einem Ausgang dürfen max. zehn Eingänge parallel angeschalten werden | |||||||||||||||||||||||||||||||||
| Ausgänge von Logikgattern werden typischerweise nicht parallel geschalten - nur besondere Bauelemente lassen dies zu (Tri-State-Ausgänge und Open Colector) und es liegt auch nur selten eine wirkliche Notwendigkeit dazu vor (Bildschirmansteuerungen mit RGB-Signalen sind aber solche Ausnahmefälle) | |||||||||||||||||||||||||||||||||
| Linkliste | |||||||||||||||||||||||||||||||||
A ۷ B Vereinigung der Mengen A und B |
| 0. Bool'sche Algebra und deren technische Umsetzung |
|
|
|
| George Boole - englischer
Mathematiker Hier nun muss notwendigerweise der ganze mathematische Randkimskrams aufgeführt werden, der aus tausenden Formeln besteht und von keinem im Normalfall wirklich gelesen. Wenn man allerdings ein Projekt in diesem Sinne am Backen hat, dann sieht die Sache ganz anders aus. |
|
|
Prinzipien der klassischen Aussagenlogik. Als Aussagen bezeichnet man
bestimmte sprachliche Gebilde, die zur Beschreibung und Mitteilung von
Sachverhalten dienen. Die klassische Aussagenlogik geht von zwei
Voraussetzungen aus. Nach dem Prinzip der Zweiwertigkeit ist jede Aussage entweder wahr oder falsch. Der hierbei verwendete, auf ARISTOTELES zurückgehende Wahrheitsbegriff bezeichnet eine Aussage dann als wahr, wenn der in ihr behauptete Sachverhalt zutrifft. Das Prinzip der Zweiwertigkeit enthält zwei Prinzipien: 1. Das Prinzip vom ausgeschlossenen Dritten, nach dem jede Aussage wahr oder falsch ist; und 2. das Prinzip vom ausgeschlossenen Widerspruch, nach dem es keine Aussage gibt, die sowohl wahr als auch falsch ist. Die Klasse aller Aussagen zerfällt damit in zwei Teilklassen, die durch die Symbole 1 (wahr) und 0 (falsch) bezeichnet und Wahrheitswerte genannt werden. Mit Hilfe sprachlicher Partikel, z. B. „nicht", „und", „oder", lassen sich gegebene Aussagen zu komplizierteren Aussagen zusammensetzen. Nach dem zweiten Grundprinzip, dem Extensionalitätsprinzip, ist der Wahrheitswert einer zusammengesetzten Aussage ausschließlich durch die Wahrheitswerte ihrer Komponenten bestimmt und hängt nicht von deren Sinn ab. Infolgedessen lassen sich derartige Verknüpfungen als Funktionen deuten, die n-Tupeln von Wahrheitswerten wieder Wahrheitswerte zuordnen. Die für die Aussagenlogik gebräuchlichsten Verknüpfungspartikel, ihre Bezeichnung und die ihnen jeweils entsprechende Wahrheitsfunktion sind Verknüpfungs- Schreibweise Benennung zugeordnete partikel in Funktoren Wahrheitsfunktion nicht --i Negation non und A Konjunktion et oder v Alternative vel wenn ..., so -> Implikation seq genau dann ..., wenn H Äquivalenz aeq Die Wahrheitsfunktionen, p non p p q et (p, q) vel (p, q) seq (p, q) aeq (p, q) deren Argumente und Funktionswerte Wahrheitswerte sind, lassen sich am einfachsten durch ihre Funktionstafeln Darstellung von Funktionen beschreiben 1 0 1 1 1 1 1 1 |
|
|
|
| 1. Allgemeines zur Logik und Kombinatorik |
|
|
|
| Hier nun muss notwendigerweise der ganze mathematische Randkrimskrams aufgeführt werden, der aus tausenden Formeln besteht und von keinem im Normalfall wirklich gelesen. Wenn man allerdings ein Projekt in diesem Sinne am Backen hat, dann sieht die Sache ganz anders aus. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Klemmverhalten logischer Schaltungen mit zwei Eingängen und einem Ausgang: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 2. Allgemeines zur Logik und Kombinatorik |
|
|
|
| Grundsatz logischer
Schaltungen: gleicher Input erzeugt immer gleichen Output! Logik
ist kein mathematisches Problem sondern eine Frage der Definition und Zuordnung! |
||
|
||
|
allgemeines
Blockschaltbild logischer Schaltungen |
||
| Hier und jetzt folgen die einigen wenigen und wirklich wichtigen Sätze der Logik - beherzige sie einfach - sie sind einfach: | ||
| zur Entwicklung logischer Gesamtaussagen werden jeweils nur die wahren oder falschen Aussagen herangezogen und entsprechend logisch verknüpft | ||
| alle Einzelaussagen werden UND bzw. ODER-verknüpft - sie müssen ja in ihrer Gesamtheit eine wahre Aussage ergeben - alle wahren Aussagen gemeinsam werden UND bzw. ODER-verknüpft | ||
| mittels der de Morgan'schen Theoreme lassen sich Aussagen verkürzen - und interessanterweise auch logisch umkehren, was für den Bauelemente-Einsatz sehr bedeutsam ist | ||
| Schaltungstechnische Realisierung ist aber nur möglich, wenn die Aussage nicht einen Widerspruch in sich enthält, d. h. die logischen Bedingungen dürfen nicht so gestellt sein, das überhaupt keine Aussage möglich ist | ||
| mehrere wahre logische Aussagen werden logisch ODER verknüpft | ||
| Logikschaltungen sind der technische Ansatz zu dem, was wir Künstliche Intelligenz nennen - 's gibt natürlich auch künstliche (... sowie vor allem auch natürliche) Dummheit!!! ;-) | ||
| ... und so wird eine Logik entwickelt |
| 3. De Morgan'sche Theoreme |
|
|
|
| Das nunmehr folgende sind Geheimwaffen der Logikinterpretation und gleichzeitig eigentlich die Kürzungsregeln der Logik. Sie sind klein, es sind nur wenige (also eigentlich nur zwei), aber in denen steckt das Potential zu Ermittlung des IQ's. | |
|
Die
de Morganschen Gesetze der
Aussagenlogik lauten: NICHT (A UND B) = NICHT A ODER NICHT B NICHT (A ODER B)
= NICHT A UND NICHT B. |
|
| 4. Schaltungslogik - Torschaltungen |
|
|
|
|
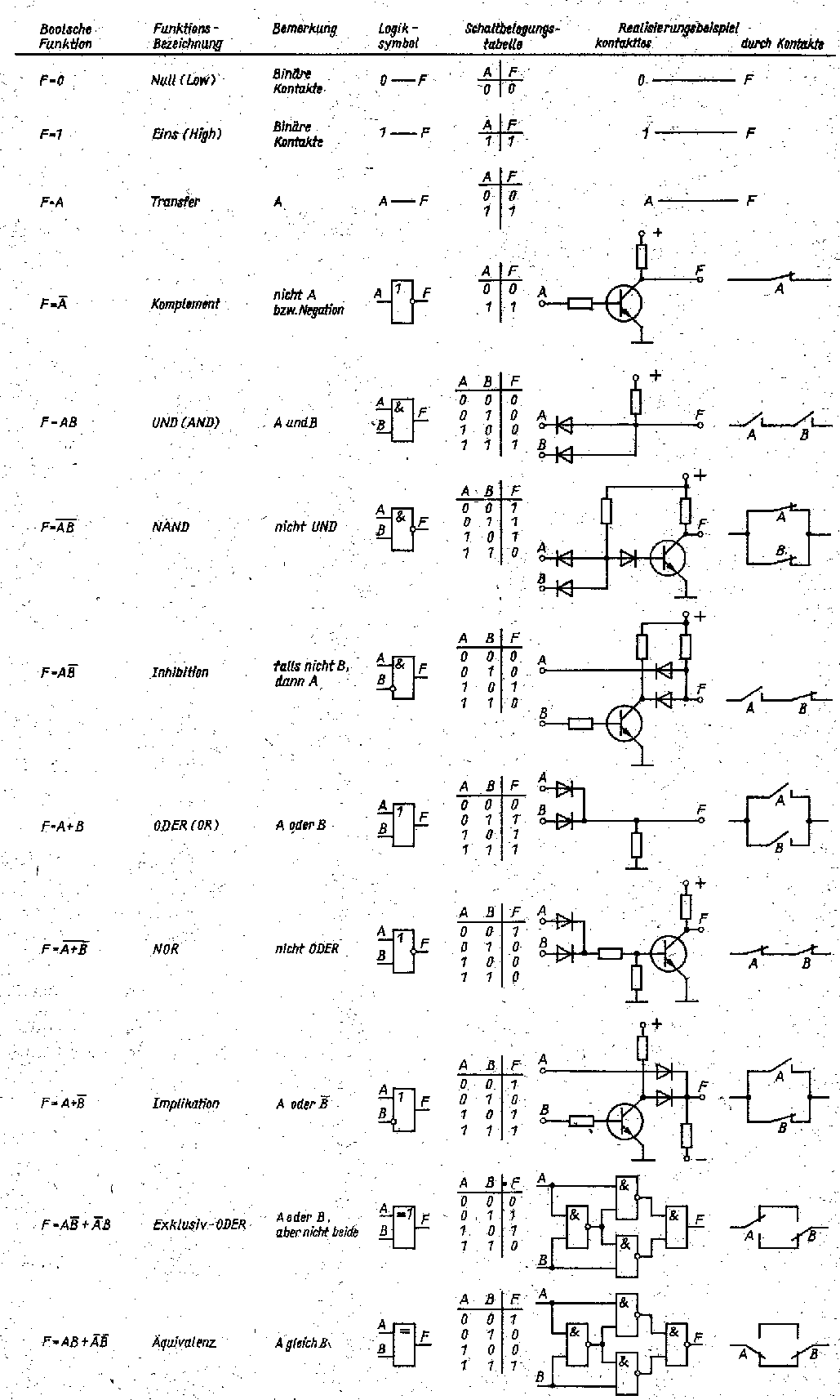
Logische Gatter sind die elementaren Grundbausteine digitaler Schaltungen und
Systeme. Sie steuern den Signalfluss durch das gesamte digitale System. Die
Bezeichnung Gatter (Tor) weist darauf hin, dass sie durch die am Eingang anliegenden Signale geöffnet
und geschlossen werden können und auf diese Weise entweder die Information
weiterleiten oder ihre Weiterleitung verhindern. Wir betrachten in diesem Buch ausschließlich
Elemente der zweiwertigen (binären) Logik. Mit nur einem Gattertyp, der eine Verknüpfungsform und eine Negation enthält (z. B. NAND- oder NOR-Gatter) lassen sich alle digitalen Steuerungsfunktionen, d. h. sowohl Kombinations- als auch Folgeschaltungen realisieren. Selbst der umfangreichste Digitalrechner lässt sich (theoretisch) aus einem oder aus wenigen immer wiederkehrenden Grundgattern aufbauen. Aus Aufwandsgründen werden in der Praxis jedoch überwiegend hoch- und höchstintegrierte Schaltkreise (RAMs, ROMS, ALU, Multiplizierer u. a. m.) verwendet. Aus logischer Sicht realisiert jedes elementare Grundgatter (z. B. UND, ODER, NAND, NOR, Negator) eine kombinatorische Verknüpfung. Durch Zusammenschalten mehrerer Grundgatter und Anwenden des Prinzips der Rückkopplung entstehen Folgeschaltungen. Die logische Funktion von Gattern (d. h. die logische Abhängigkeit zwischen den Ausgangs- und den Eingangssignalen) wird mit Hilfe der Schaltalgebra (Boolesche Algebra) beschrieben. Die Gleichungen der Booleschen Algebra sind darüber hinaus für den Entwurf digitaler Schaltungen und Systeme sowie für deren Vereinfachung (Minimierung der Anzahl von Gattern) von großer Bedeutung. Im vorliegenden Abschnitt geben wir einen Überblick über allgemeine Eigenschaften und Kenngrößen logischer Grundgatter. Auf die statische und dynamische Berechnung von Transistorstufen und von Gattern wollen wir verzichten, da dies in zunehmendem Maße Anliegen des Schaltkreisherstellers ist. In digitalen Schaltkreisen werden die beiden logischen Signalwerte 0 und 1 nahezu ausnahmslos durch zwei unterschiedliche Spannungspegel (H-Pegel und L-Pegel) dargestellt (darüber hinaus muss zwischen statischen und dynamischen Logiksystemen unterschieden werden. Die beiden Pegelwerte (exakter: Pegelbereiche) bezeichnet man mit HIGH (H)-Pegel: Pegelwert ist näher bei + 5Volt. LOW (L)-Pegel: Pegelwert ist näher bei - 0 Volt. Diese allgemeine Bezeichnung der beiden Pegelwerte hat den Vorteil, dass die konkreten (und bei den zahlreichen Schaltkreisfamilien unterschiedlichen) Pegelwerte hierbei aus Gründen der Allgemeingültigkeit umgangen werden können. |
|||||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||

|
|||||||||||||||||||||
|
|||||||||||||||||||||
| 5. Verwandte Themen |
|
|
|
|
|
Aussagenlogik, Logik und Kombinatorik, Kanonische Normalformen - aber auch die Gesetze zur logischen Schaltungsentwicklung sowie auch ihre Vereinfachung spielen alle in diese Feld der Grundlagen. Hier einige Tipps, um diese näher zu beschnuppern, oder daran vollkommen zu verzweifeln. | ||||||||||||||||
|
|
| 6. Weblinks |
|
|
|
|
|
Also los - machen wir Aussagenlogik und versuchen wir, deduktiv zu folgern: das ist dann eigentlich schon ein Spezialgebiet der Kombinatorik. |
| http://www.tfh-berlin.de/~msr/pdf-files/VL4.PDF |
| 7. Übungsaufgaben |
|
|
|
|
|
Also los - machen wir Aussagenlogik und versuchen wir, deduktiv zu folgern: das ist dann eigentlich schon ein Spezialgebiet der Kombinatorik. |
Witz des Themas:
Im Wartezimmer eines Nervenarztes führt sich einer wie Tarzan auf.
Fragt ein anderer: “Wer hat Ihnen eigentlich gesagt, dass Sie Tarzan sind?”
Im Brustton der Überzeugung kommt die Antwort: “Der liebe Gott.”
Da steht in der Ecke des Zimmers ein dritter auf und fragt: “Was soll ich gesagt
haben?”
|
zur Hauptseite |
© Samuel-von-Pufendorf-Gymnasium Flöha | © Frank Rost im Januar 1996 |
|
... dieser Text wurde nach den Regeln irgendeiner Rechtschreibreform verfasst - ich hab' irgendwann einmal beschlossen, an diesem Zirkus nicht mehr teilzunehemn ;-) „Dieses Land braucht eine Steuerreform, dieses Land braucht eine Rentenreform - wir schreiben Schiffahrt mit drei „f“!“ Diddi Hallervorden, dt. Komiker und Kabarettist |
|
Diese Seite wurde ohne Zusatz irgendwelcher Konversationsstoffe erstellt ;-) |