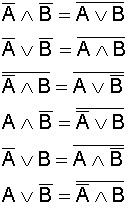|
Eine Hauptaufgabe der
mathematischen Logik ist die Untersuchung des formalen Denkens und
Schließens mit Hilfe mathematischer Methoden, die z. B. der Algebra und der
Algorithmentheorie entnommen sind.
Diese ursprünglich aus der Philosophie stammende Aufgabe ist jedoch nicht
ihre einzige; die mathematische Logik umfasst heute eine Vielzahl von
Fragestellungen und Anwendungen auf den verschiedensten Gebieten, z. B. in
den Naturwissenschaften, in der Schaltalgebra, in der Theorie
informationsverarbeitender Systeme, in der Linguistik und in verschiedenen
Disziplinen der Gesellschaftswissenschaften wie Philosophie,
Rechtswissenschaft und Ethik.
Entscheidende Impulse für die Entwicklung der mathematischen Logik ergaben
sich aus der Situation der Mathematik am Ausgang des 19. Jahrhunderts. Diese
hatte bis dahin eine Fülle einzelner Resultate gesammelt und schon einen
hohen Abstraktionsgrad erreicht, ohne dass über den Inhalt der intuitiv
verwendeten Grundbegriffe, z. B. des Mengenbegriffs und des logischen
Schließens, ausreichende Klarheit bestand. Neben dem Bedürfnis nach einer
zweifelsfreien Begründung des Mengenbegriffs ergab sich zum ersten Male die
Notwendigkeit einer Einsicht in das, was Logik und logische Deduktion
eigentlich bedeuten. |
 |
|
Die de Morgan'sche
Konvertierung
|
Die Regeln zur Umwandlung eines
Schaltterms nach de Morgan |
Um einen Schaltterm nach de Morgan umzuwandeln,
müssen
1. die Teilterme negiert (invertiert) werden, wobei sich
doppelte Negierung aufhebt, und
2. die Gatter wie folgt umgewandelt
werden: 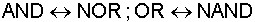
|
|
Umwandlung von Beispieltermen nach de
Morgan |
|
|
Beweis der Beispiele durch
Wahrheitstabellen |
|
|
|
|
|
X |
|
Y |
|
Nr. |
B |
A |
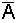 |
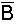 |
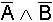 |
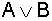 |
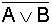 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
2 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
3 |
1 |
1 |
0 |
0 |
0 |
1 |
0 | |
|
|
|
|
|
X |
|
Y |
|
Nr. |
B |
A |
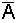 |
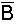 |
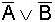 |
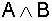 |
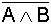 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
2 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
3 |
1 |
1 |
0 |
0 |
0 |
1 |
0 | |
|
|
|
|
X |
|
|
Y |
|
Nr. |
B |
A |
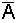 |
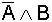 |
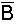 |
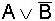 |
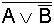 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
|
2 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
3 |
1 |
1 |
0 |
0 |
0 |
1 |
0 | |
|
|
|
|
X |
|
|
Y |
|
Nr. |
B |
A |
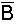 |
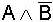 |
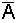 |
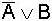 |
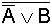 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
2 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
3 |
1 |
1 |
0 |
0 |
0 |
1 |
0 | |
|
|
|
|
X |
|
|
Y |
|
Nr. |
B |
A |
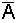 |
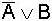 |
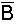 |
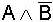 |
 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
|
2 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
3 |
1 |
1 |
0 |
1 |
0 |
0 |
1 | |
|
|
|
|
X |
|
|
Y |
|
Nr. |
B |
A |
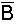 |
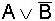 |
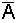 |
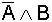 |
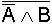 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
2 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
3 |
1 |
1 |
0 |
1 |
0 |
0 |
1 | |
In
allen Fällen ist hier X = Y, d.h. die jeweils zusammengehörenden Terme
sind gleich und somit die de Morgan'schen Regeln
bewiesen.
|
|
Darstellung der Grundgatter nur durch
NAND- bzw. NOR-Gatter |
| Grundgatter |
NOT |
AND |
OR |
NAND |
NOR |
| Ausgangsterm |
|
|
|
|
|
| NAND-, |
|
|
|
|
|
| NOR-Darstellung |
|
|
|
|
|
|
|
Erläutertes Beispiel
|
Folgender Term soll nur durch NAND-Gatter dargestellt
werden:
|
|
|