Das K-Farben-Problem - Duden Informatik S. 237

Letztmalig dran rumgefummelt: 14.04.22 09:53:14

	Grundsätzlich besteht die Aufgabe darin, angrenzende Flächen oder benachbarte Knoten, welche durch eine Kante miteinander verbunden sind, mit einer minimalen Anzahl von verschiedenen Farben zu füllen.
	1. Problembeschreibung 2. Hintergründe und Zusammenhänge - Einordnung in Klassen 3. Anwendungsbeispiele 4. Programmvorschläge 5. Chromatische Zahl 6. Weiterführende Literatur 7. Linkliste zum Thema 8. Verwandte Themen
	Probleme & Problemlösungsverfahren Logo für das K-Farben-Problem begrenzt verwendbar - selbst aufpassen, ab welcher Stelle es Blödsinn wird ;-) Informatik-Profi-Wissen
	Quellen: Lehr- und Übungsbuch Informatik Band 1 - 5 Seite ??? Technische und Theoretische Informatik  Seite ???

1. Problembeschreibung

Die Bestimmung der chromatischen Zahl eines Graphen ist NP-schwer, das heißt, dass es – aus Sicht der Komplexitätstheorie – vermutlich keinen Algorithmus gibt, der dieses Problem effizient löst. Die Bestimmung der chromatischen Zahl ist auch eines der Probleme von Karps 21 NP-vollständigen Problemen und damit eines der ersten Probleme, für die die NP-Vollständigkeit gezeigt wurde. Ausnahmen sind bipartite Graphen und perfekte Graphen. Das Entscheidungsproblem, ob ein gegebener Graph bipartit ist, besitzt lineare Zeitkomplexität, und ist zum Beispiel mit Tiefensuche lösbar. Bei perfekten Graphen existieren Polynomialzeitalgorithmen zur Berechnung der chromatischen Zahl. Das Knotenfärbungsproblem ist NP-vollständig. Der zurzeit praktisch beste Algorithmus zur Bestimmung einer Knotenfärbung beruht auf einem Spalten-Generierungs-Ansatz. Weiterhin gibt es viele Färbungsheuristiken, die nach bestimmten Methoden gute Färbungen suchen und somit im Erfolgsfall eine obere Schranke für die chromatische Zahl liefern.

2. Hintergründe, Zusammenhänge - Einordnung in Klassen

Eines der klassischen Probleme der Graphentheorie ist die Frage, wie viele Farben man minimal braucht, um eine Landkarte so zu färben, dass je zwei aneinandergrenzende Länder nicht dieselbe Farbe haben. Dieses Problem lässt sich leicht in ein Knotenfärbungsproblem überführen. Die graphentheoretisch äquivalente Frage lautet also: Was ist die chromatische Zahl eines planaren Graphen? Der Vier-Farben-Satz besagt, dass die chromatische Zahl eines planaren Graphen höchstens 4 ist. Enthält der Graph kein Dreieck, so ist er sogar 3-Knoten-färbbar. Trotzdem ist auch für planare Graphen das Bestimmen der chromatischen Zahl NP-schwer.

3. Anwendungsbeispiele

Eine Färbung eines ungerichteten Graphen ordnet jedem Knoten bzw. jeder Kante im Graphen eine Farbe zu. In der Graphentheorie beschäftigt man sich meist nur mit sogenannten „zulässigen“ oder „gültigen“ Färbungen (siehe unten), und versucht, Algorithmen zu entwickeln, die für einen vorgegebenen Graphen eine gültige Färbung mit möglichst wenigen Farben finden. Probleme aus der diskreten Mathematik, aber auch außermathematische Fragestellungen lassen sich manchmal in ein Färbungsproblem übersetzen, daher ist die Existenz oder Nichtexistenz solcher Algorithmen auch außerhalb der Graphentheorie von Interesse.

Europa-Karte ohne Lösungsansätze für das K-Farben Problem Eingefärbte Europa-Karte Eingetragene Knotenpunkte für benachbarte europäische Länder   Europa-Karte ... zum Download im CorelDraw 11.0-Format Europa-Karte coloriert ... zum Download im CorelDraw 11.0-Format Europa-Karte mit eingetragenen Nodes ... zum Download im CorelDraw 11.0-Format

4. Programmvorschläge

	Diese Lösung stammt von Johannes Uhlig aus dem Jahr 2007 als Projektarbeit im Grundkurs Informatik. Alle zu verarbeitenden Parameter werden nochmals diskutiert und aufgerollt.
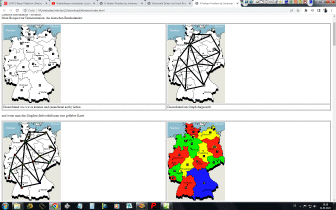	Programmierprojekt "K-Farbenproblem" nach Johannes Uhlig aus 2007

5. Chromatische Zahl

6. Weiterführende Literatur

7. Links zum Thema

8. Verwandte Themen

	Das Vorangestellte hilft wirtschaften, löst jedoch kein einziges Problem (allerdings ohne Beachtung der Worst-Case-Strategien wird man auch nicht erfolgreich Software entwickeln und/oder informatische Projekte realisieren können). Deshalb nunmehr das, was wirklich Arbeiten hilft.
	das 8-Dame-Problem des Cliquen-Problem Domino-Problem das Entscheidbarkeitsproblem das Erfüllbarkeitsproblem die Fibonacci-Zahlen das Flaggenproblem das Halteproblem das Hamilton-Problem der Kaprekar-Algorithmus die Magischen Quadrate das PASCAL'sche Dreiecksproblem das Philosophenproblem das Königsberger-Brückenproblem das Post'schen Korrespondenzproblem das Rucksackproblem das Rundreiseproblem das Springer-Problem die Türme von Hanoi das Wortproblem das Wüstenfit-Problem
	Worst-Case-Denken Algorithmentheorie Komplexität, Mächtigkeit und Aufwand Praktische Elementaralgorithmen Lösbarkeit und Problemlösungsstrategien Klassische algorithmisch lösbare Probleme Zufall und Computer Graphentheorie Petri-Netze
	Informationsbegriff Logo für die Signale Nachrichten Wissen Systembegriff Modellbegriff Simulation Denken und Sprache Zahlen, Daten und Datentypen Gegenläufigkeit und Verklemmung Pattern-Matching NP-vollständigen sowie NP-schweren Probleme

zur Hauptseite

© Samuel-von-Pufendorf-Gymnasium Flöha

© Frank Rost im April 2003