Das K-Farben-Problem (oder auch Graphenfärbungsproblem)
Es existiert ein Graph und dessen Eckpunkte sollen mit verschiedenen Farben so eingefärbt werden, dass alle Eckpunkte die durch eine Kante verbunden sind eine andere Farbe erhalten. Dabei ist die Anzahl der Farben minimal zu halten.
Die historische bedeutungsvollste und wohl berühmteste Beispiel ist die
Färbung
politischer Landkarten. Wie bekommt man aber aus einer Landkarte einen Graphen?
Indem man in jedem Land einen Knoten platziert und alle Knoten von benachbarten
Ländern miteinander verbindet.
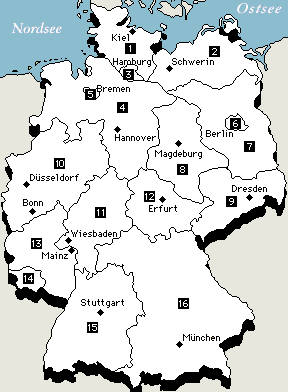
Mein Beispiel zur Demonstration: die deutschen Bundesländer:
 |
 |
| Deutschland wie wir es kennen und (manchmal auch) lieben | Deutschland als Graph dargestellt |
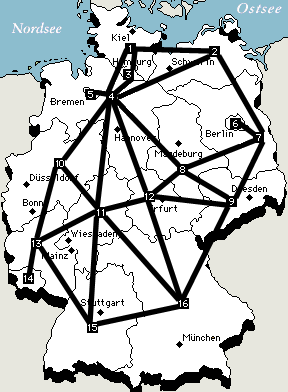
und wenn man den Graphen färbt erhält man eine gefärbte Karte
 |
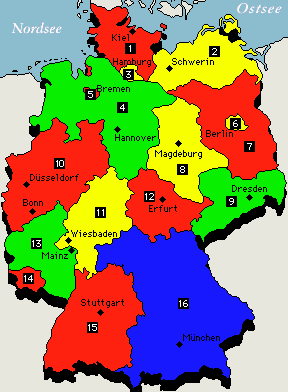 |
| so sieht der gefärbte Graph aus | und so kann eine 4-Farben-gefärbte Deutschland-Karte aussehen |
und so sieht das ganze in meinem Programm aus (die Farben können von der Handkolorierung abweichen):
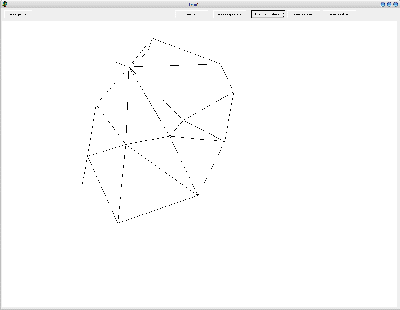 |
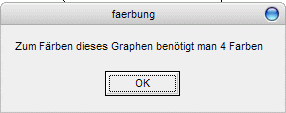 |
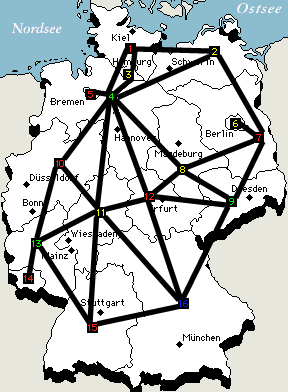
| Deutschland wie wir es kennen und (manchmal auch) lieben als Graph | Hier ist die Bestätigung, dass man 4 Farben benötigt |
und dann erählt man:
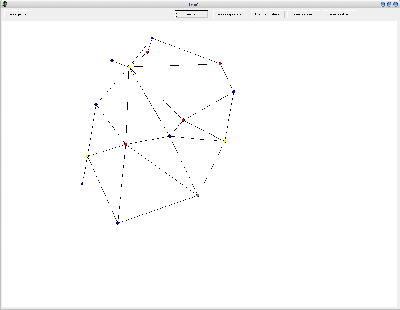 |
| so sieht der gefärbte Graph aus wenn er aus dem Programm kommt (klicken zum Vergrößern) |
HIER kann man die gespeicherte Graphendatei der Deutschlandkarte herunterladen.
Gibt es aber praktische Anwendungen dafür, die man noch benötigt?
Ja, die gibt es: ein Beisiel, dass jeder verstehen wird ist das der Handysender. Man hat viele Handysender aufgestellt. Alle, deren Reichweite sich überschneiden (und das sind alle benachbarten, da es sonst Funklöcher gibt) müssen auf unterschiedlichen Frequenzen senden, da es sonst zu störenden Interferenzen kommt. Nun kann man jeden Handysender als Knoten betrachten und alle die sich überschneiden mit einer Linie verbinden. Färbt man diesen Graph nun durch so wenige Farben wie möglich erkennt man welcher Sender auf welcher Frequenz senden muss. Die Anzahl der Farben und Frequenzen ist minimal zu halten, da Sender mit verschiedenen Frequenzen teurer sind.
Beispiel: Ebenfalls nachzulesen auf Rosts Webseiten:
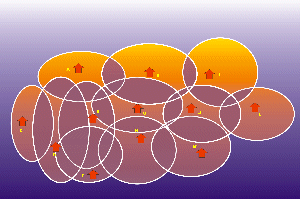 |
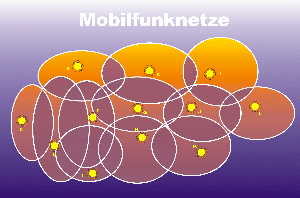 |
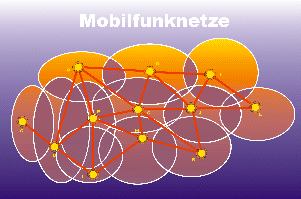
| Die Sendestationen mit Reichweiten | Jeder Sender als ein Knoten dargestellt |
 |
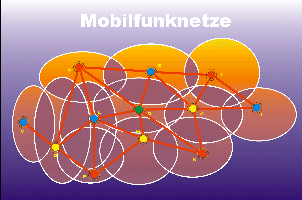 |
| Sender, die sich überlagern werden mit Kanten verbunden | Und gefärbt siehr das so aus |
 |
| Und wenn wir wieder die Sendestationen betrachten sieht das so aus |
HIER gibt es das erste Bild als Hintergrunddatei für das Programm
Eine weitere Anwendung ist die Stundenplanproblematik. Da muss man jeder Klasse und jedem Lehrer bestimmte Ereignisse als Knoten zuweisen und kann dann daraus einen Stundenplan erstellen. Dieses System ist aber extrem kompliziert, weshalb Software, die dieses System anwendet auch so sündhaft teuer ist.
Die Hanhabung ist (wie immer bei meinen Programmen) kinderleicht. Zumindest für mich. Aber mal Scherz beiseite, so geht es wirklich:
Öffnen:
Zu Beginn solte man das Programm ausführen. Dazu kann man wahlweise die Datei "faerbung.exe" oder das Delphi-Projekt "faerbung.zip", nachdem man es entpackt hat, benutzen.
die leere Anwendung:
Die leere Anwendung präsentiert sich nach dem Start folgendermaßen:
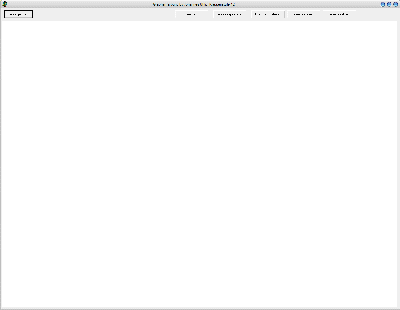 |
| die Anwendung im Startzustand (klicken zum Vergrößern) |
erste Schritte:
nun kann durch linksklicken in den weißen Teil des Feldes (ist eigentlich die ganze Anwendung) den Startpunkt festlegen und dann durch einen weiteren Linksklick eine erste Linie des Graphen ziehen:
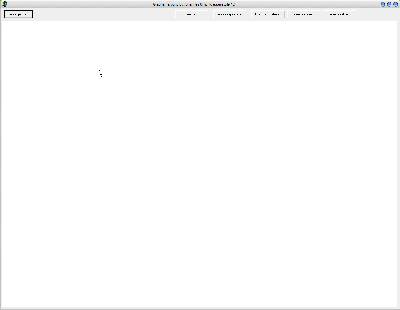 |
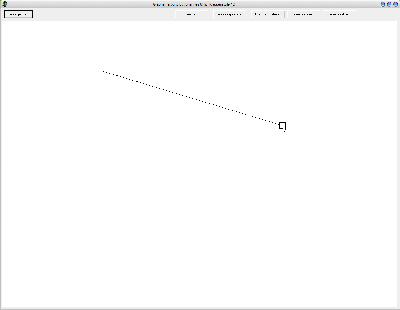 |
| So sieht es aus, wenn man den Startpunkt definiert hat (klicken zum Vergrößern) | Und so wenn die erste Linie da ist (klicken zum Vergrößern) |
Linien werden immer vom Endpunkt der letzten Linie aus gezogen. Den muss man sich merken oder man verwendet die rechte Maustaste.
Auf diese Art und Weise kann man nun seinen gesamte Graphen aufbauen. Um Knoten zu ermöglichen habe ich die Fangfunktion integriert. Diese funktioniert so, dass wenn man den Mauszeiger in die Nähe eines End- / Anfangspunktes einer Linie bewegt ein Viereck auftaucht. Klickt man nun auf dieses wird der Eckpunkt gefangen und die Verbindung im Graphen hergestellt. Falls doch mal etwas danebengeht kann man auch rückgängig schalten.
Die rechte Maustaste kann man verwenden um den Startpunkt einer Linie zu definieren.
Dies kann zum Beispiel nützlich sein, wenn man vergessen hat, wo der letzte
Endpunkt war oder wenn man an einem anderen Ende des Graphen weiterzeichnen
will. Dabei ist zu BEACHTEN, dass diese Funktion nur funktioniert, wenn man
auf einen anderen Knoten mit der rechten Maustaste klickt und dieser durch
den Fang angewählt wurde.
Das heißt: Man kann nur den Startpunkt der Linie wechseln indem man auf das Viereck,
dass an einem anderen Knoten entsteht, wenn man mit der Maus in seine Nähe kommt,
mit der rechten Maustaste anklickt.
| Beispiel | Gegenbeispiel |
 |
 |
| Hier wird die Spitze des Gebildes neuer Linienstartpunkt (klicken zum Vergrößern) | Hier bleibt der alte Startpunkt gesetzt (klicken zum Vergrößern) |
Färben des Graphen:
Das Färben des Graphen ist denkbar einfach. Man muss nur auf die Schaltfläche "faerben" und nach kurzer Zeit erhält man den gefärbten Graph und eine Meldung wie viele Farben nötig waren.
Im- und Exportieren:
Speichern, und somit auch Laden, kann man nur die Graphen, nicht die Färbund dazu, da ja sonst der ganze spaß verloren gehen würde.
Grenzen des Programms:
Das Programm lässt auch Kreuzungen zu ohne dabei Knoten zu erzeugen. Das ist zwar unlogisch, wenn man sich das Beispiel mit den Mobilfunknetzen als Grundlage wählt, macht aber einen Sinn, wenn man zum Beispiel die Stundenplan-Problematik aussucht.
Ergebnisse:
Hier ein paar Ergebnisse (links als Bild und rechts zum Download als TXT-Datei, Bitte Rechtsklick und dann Ziel speichern unter)
 |
 |
| so sieht der gefärbte Deutschland-Graph aus wenn er aus dem Programm kommt (klicken zum Vergrößern) | Download des Deutschland-Graphen |
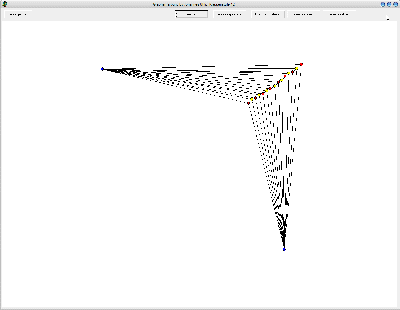 |
 |
| so sieht der gefärbte Graph aus wenn er aus dem Programm kommt (klicken zum Vergrößern) | Download des Graphen |
Nur für den Herrn Rost gibt es hier unten den Quelltext der Hauptprozedur zum angucken:
procedure TForm1.Button3Click(Sender:
TObject); //faerben-button
var
b3i:Integer;
Knoten: TComponent;
begin
anzfarben:=0;
ListBox3.Items.Clear;
ListBox4.Items.Clear;
If ogalt>0 then
begin
For b3i:=0 to ogalt-1 do
begin
Knoten:=FindComponent('Knoten_gef' +IntToStr(b3i));
Knoten.Destroy;
end;
end;
For b3i:=0 to 10000 do
begin
farbe[b3i]:=0;
end;
start:=0;
faerben(start);
ListBox5.Items.Clear;
For b3i:=0 to og-1 do
begin
ListBox5.Items.Add(intToStr(farbe[b3i]));
Knoten_gef:=TShape.Create(self);
Knoten_gef.Parent:=self;
Knoten_gef.Shape:=stCircle;
Knoten_gef.Name:='Knoten_gef'+IntToStr(b3i);
Knoten_gef.Brush.Color:=farbuebersetzung[farbe[b3i]];
Knoten_gef.SetBounds(Image1.Left+corner[b3i,1]-5,Image1.Top+corner[b3i,2]-5,10,10);
end;
ogalt:=og;
ShowMessage('Zum Färben dieses
Graphen benötigt man '+IntToStr(anzfarben)+'
Farben');
end;
procedure TForm1.faerben(f_ecke:integer); //die
hautpprozedur
begin
f_j:=0;
for f_i:=0 to lineog-1 do //heraussuchen aller Ecken um die Aktuellen
begin
If ((corner[f_ecke,1]=line[f_i,1]) and (corner[f_ecke,2]=line[f_i,2])) then
begin
f_tempkoord[f_j,1]:=line[f_i,3];
f_tempkoord[f_j,2]:=line[f_i,4];
inc(f_j,1);
end;
If ((corner[f_ecke,1]=line[f_i,3]) and (corner[f_ecke,2]=line[f_i,4])) then
begin
f_tempkoord[f_j,1]:=line[f_i,1];
f_tempkoord[f_j,2]:=line[f_i,2];
inc(f_j,1);
end;
end;
For f_k:=0 to f_j-1 do //heraussuchen der Nummern der Ecken um die Farben zu überprüfen
begin
ListBox3.Items.Add(IntToStr(f_tempkoord[f_k,1])+','+IntToStr(f_tempkoord[f_k,2]));
//testen
For f_l:=0 to og-1 do
begin
If ((corner[f_l,1]=f_tempkoord[f_k,1]) and (corner[f_l,2]=f_tempkoord[f_k,2]))
then
begin
f_tempnumber[f_k]:=f_l;
break;
end;
end;
ListBox4.Items.Add(IntToStr(f_tempnumber[f_k])); //testen
end;
f_geht:=false;
while f_geht=false do
begin
inc(farbe[f_ecke],1);
If farbe[f_ecke]>anzfarben then
begin
anzfarben:=farbe[f_ecke];
end;
f_geht:=testen(f_ecke,f_tempnumber,f_j-1);
end;
If (f_ecke<og-1) then
begin
faerben(f_ecke+1);
end;
end;
für alle die hier nicht fündig wurden gibt's hier das Projekt.
Und hier noch mal die Downloads der Datei "faerbung.exe" oder des Delphi-Projekts "faerbung.zip"