Das Hamster-Teiler-Problem

Letztmalig dran rumgefummelt: 01.01.08 12:18:23

	Die Hamster Knabberzähnchen, Goldfellchen und Weißbrüstchen haben einen Haufen Weizenkörner gesammelt, den sie am nächsten Tag untereinander aufteilen wollen. Nachts wacht Knabberzähnchen auf und beschließt, sich seinen Teil schon beiseite zu legen. Es teilt die Weizenkörner in drei gleich große Haufen auf. Ein Korn bleibt dabei übrig. Mäuschen Piep, das gerade aus seinem Loch gekommen ist, holt sich dieses Korn. Nachdem Knabberzähnchen seinen Anteil versteckt hat, legt es die anderen Weizenkörner wieder zu einem Haufen zusammen und schläft weiter. Jetzt aber wacht Goldfellchen auf und beschließt ebenfalls, sich seinen Anteil schon zu nehmen. Auch diesmal bleibt ein Korn für Piep übrig. Nachdem Goldfellchen wieder eingeschlafen ist, wacht Weißbrüstchen auf, teilt den noch vorhandenen Haufen in drei gleiche Teile, wobei wiederum ein Weizenkorn für Piep übrigbleibt. Weißbrüstchen nimmt sich einen Teil und legt die anderen beiden wieder zu einem Haufen zusammen. Am nächsten Morgen beschließen die drei misstrauischen Hamster, den Resthaufen zu teilen. Wieder ergeben sich drei gleiche Teile und ein Korn für Piep. Martin hört von dieser Geschichte und fragt sich: Wieviel Weizenkörner enthielt der Haufen am Abend vorher? Wie viel Weizenkörner hatte jeder der drei Hamster am Morgen nach der letzten Teilung?
	1. Problembeschreibung 2. Hintergründe und Zusammenhänge - Einordnung in Klassen 3. Lösungsalgorithmen 4. Programmvorschläge 5. Zusammenfassung 6. Weiterführende Literatur 7. Linkliste zum Thema 8. Verwandte Themen
	Praktische Elementaralgorithmen Logo für die Hamsterteilerei begrenzt verwendbar - selbst aufpassen, ab welcher Stelle es Blödsinn wird ;-) Wissen für Fortgeschrittene der Informatik
	Quellen: Summa Summarum - Kostproben unterhaltsamer Mathematik Seite 34 ff.

1. Problembeschreibung

	x sei die Anzahl der von allen gesammelten Weizenkörner; und u, v, w seien die Anzahlen der Körner, die sich jeweils Knabberzähnchen, Goldfellchen und Weißbrüstchen nachts zurücklegen; y sei die Anzahl der Körner, die jeder bei der morgendlichen Teilung erhält.
	Der Kornhaufen wurde insgesamt viermal aufgeteilt. Wir erhalten dabei der Reihe nach folgende vier Gleichungen: x = 3u + 1, 2u = 3v + 1, 2v = 3w + 1, 2w = 3y + 1. Lösen wir die letzte Gleichung nach w auf und setzen sie in die vorletzte ein usw., so erhalten wir schließlich 8x = 81y + 65.
	Nach Division durch 8 lautet die Gleichung
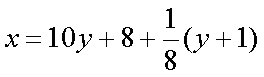	Damit x ganzzahlig wird, muss y + 1 ein Vielfaches von 8 sein. Entsprechend der Aufgabenstellung soll außerdem x > 0 und y > 0 gelten. Die kleinste mögliche Lösung erhalten wir für y = 7. Dann ist x = 79. Weitere Lösungen bekommen wir, wird y = 15, 23, 31, ... gesetzt. Für die Größe des gesamten Haufens ergibt sich in diesen Fällen x = 160, 241, 322, ... Wir wollen annehmen, dass die drei Hamster 79 Weizenkörner sammelten. Dann haben am Ende Knabberzähnchen 33, Goldfellchen 24 und Weißbrüstchen 18 sowie Piep 4 Körner.

2. Hintergründe, Zusammenhänge - Einordnung in Klassen

	Mit nur drei Hamstern haben wir die Lösung dieser Aufgabe schnell herausbekommen. Wie groß wird der Kornhaufen bei n Hamstern, wenn wieder bei jeder Teilung Mäuschen Piep ein Korn erhält? In diesem Falle erhalten wir die Gleichung:
	Benutzen wir die Formel
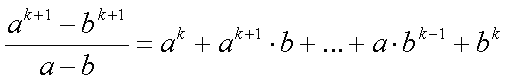	mit
	so können wir dafür kürzer schreiben
	oder
	y + 1 muss also ein natürliches Vielfaches von (n - 1)n sein, d. h. k = 1, 2, ... Weizenkörner haben n Hamster und ein Mäuschen angehäuft

3. Lösungsalgorithmus

Nimm die vorgegebene Zahl - fülle sie auf vier Stellen auf. Ergibt sich Gleichheit in allen vier möglichen Stellen, so verabschieden wir uns von der Zahl - sie ist keine Zahl innerhalb des Definitionsbereiches - was wir selbstverständlich softwartechnisch exakt wegfangen, wobei wir Oma und/oder Katze nutzen! Wir erhalten in jedem Fall der verbleibenden Restmenge vier Stellen (ungleich in mindest einer Position) und bilden daraus die jeweils kleinste und größte ziffernfolge als Zahl. Von der jeweils größeren subtrahieren wir die jeweils kleinere und verfahren damit, bis wir entweder 6174 oder eine Tiefe von 7 erreicht haben (was im Worst-Case gleichzeitig eintritt).

4. Programmvorschläge

	Hannes Uhlig hat unser Vorschläge konsequent aufgegriffen und einschließlich der Problematik Oma und Katze ein Programm des Kaprekar-Algorithmus notiert, in welchem schon einige Kerngedanken eines sauberen - eben noch nicht objektorientierten Programmieirstils zusammenlaufen.

5. Zusammenfassung

Mit Aufgaben dieser Art, die auf Gleichungen führen, für die ganzzahlige Lösungen gesucht werden beschäftigte man sich schon vor Jahrhunderten und sie tauchen in vielen alten Rechenbüchern auf. Man findet zahlreiche solche Aufgaben im zweiten Teil von L. EULERS „Vollständiger Anleitung zu Algebra" [9], die 1770 in Petersburg erstmals erschien. Wir wollen daraus die nächsten Aufgabe entnehmen und sie ähnlich wie EULER lösen, de schrieb, dass die Lösung derartiger Aufgaben „oft ganz besondere Kunstgriffe erfordert, und sehr zur Belehrung der Anfänger sowie zur Ausbildung ihrer Fertigkeit im Rechnen dient."

Knobelaufgabe: „Man suche zwei Zahlen, die so beschaffen sind, dass, wenn ihre Summe z ihrem Producte addirt wird, 79 herauskommt."

6. Weiterführende Literatur

7. Links zum Thema

8. Verwandte Themen

	Das Vorangestellte hilft wirtschaften, löst jedoch kein einziges Problem (allerdings ohne Beachtung der Worst-Case-Strategien wird man auch nicht erfolgreich Software entwickeln und/oder informatische Projekte realisieren können). Deshalb nunmehr das, was wirklich Arbeiten hilft.
	das 8-Dame-Problem des Cliquen-Problem Domino-Problem das Entscheidbarkeitsproblem das Erfüllbarkeitsproblem die Fibonacci-Zahlen das Flaggenproblem das Halteproblem das Hamilton-Problem das K-Farben-Problem der Kaprekar-Algorithmus die Magischen Quadrate das PASCAL'sche Dreiecksproblem das Philosophenproblem das Königsberger-Brückenproblem das Post'schen Korrespondenzproblem das Rundreiseproblem das Springer-Problem die Türme von Hanoi das Wortproblem das Wüstenfit-Problem das 153-Problem
	Worst-Case-Denken Algorithmentheorie Komplexität, Mächtigkeit und Aufwand Praktische Elementaralgorithmen Lösbarkeit und Problemlösungsstrategien Klassische algorithmisch lösbare Probleme Zufall und Computer Graphentheorie Petri-Netze
	Informationsbegriff Logo für die Signale Nachrichten Wissen Systembegriff Modellbegriff Simulation Denken und Sprache Zahlen, Daten und Datentypen Gegenläufigkeit und Verklemmung Pattern-Matching

zur Hauptseite

© Samuel-von-Pufendorf-Gymnasium Flöha

© Frank Rost am 26. Dezember 2007