Heron von Alexandria

Letztmalig dran rumgefummelt: 13.12.11 18:54:43

	„Es mag zwar paradox klingen, doch alle exakte Wissenschaft wird von dem Gedanken der Annäherung beherrscht!“ Bertrand Russel
	1. Heron von Alexandria 2. Das Heronverfahren 3. Lösungsalgorithmen 4. Programmvorschläge 5. Zusammenfassung 6. Weiterführende Literatur 7. Linkliste zum Thema 8. Verwandte Themen
	Praktische Elementaralgorithmen Heron von Alexandria inhaltlich auf korrektem Stand - evtl. partiell unvollständig ;-) Basiswissen der Informatik   Wissen für Fortgeschrittene der Informatik Informatik-Profi-Wissen
	Quellen: LOG IN - Heft 146/147 (2007) Seite 47 ff.

1. Heron von Alexandria

Unter allen "alten" Findern und Erfindern ist der Grieche Heron von Alexandrien als außerordentlich bemerkenswert hervorzuheben. Er war ein gelehrter Wissenschaftler, Mathematiker, Mechaniker, Physiker, Naturforscher, Techniker, Ingenieur der Antike und lebte in Alexandrien, Ägypten. Von wann bis wann er genau lebte ist unklar, ein Gelehrtenstreit, aber es war wohl in der Zeitspanne 150 v. Chr. - 250 n. Chr. Seine Schriften überlebten in griechischen, lateinischen und arabischen Übersetzungen. Sie sind eine großartige Sammlung von Ideen sowohl wissenschaftlicher als auch spielerischer Art und bilden eine Enzyklopädie der angewandten Geometrie und Mechanik.

seine Verfahren und Ideen auch auf anderen Gebieten von Naturwissenschaft und Philosophie waren bahnbrechend

2. Das Heronverfahren

	Das Heron-Verfahren (auch Babylonisches Wurzelziehen genannt) ist ein alter iterativer Algorithmus zur Bestimmung einer rationalen Näherung der Quadratwurzel einer Zahl. Es ist ein Spezialfall des Newton-Verfahrens. Die Iterationsvorschrift lautet:
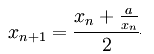	Im Folgenden ein triviales Beispiel für die Wurzel aus 9 und die Annäherung nach vier Berechnungsschritten an den wahren Wert Wurzel aus 9 =3: Näherungsschritte nach Heron-Verfahren
	Geometrische Veranschaulichung der Heron'schen Ideen Der Flächeninhalt eines Quadrates kann über das Quadrat der Länge seiner Seiten berechnet werden. Die Bestimmung der Quadratwurzel einer gegebenen Zahl a kann also geometrisch gedeutet werden als Bestimmung der Seitenlänge (genauer: als rationale Näherung zu ) eines Quadrates mit dem Flächeninhalt a. Die Idee ist, von einem Rechteck des Flächeninhaltes a auszugehen und die Seitenlängen einem Quadrat immer weiter anzunähern. Dazu wird ein Startwert gewählt, im obigen Fall gilt a = 9 und als Startwert wurde x0 = 1 gewählt. Geometrisch bedeutet dieses, dass von einem Rechteck der Seitenlänge x0 = 1 ausgegangen wird. Die andere Seitenlänge dieses Rechtecks ergibt sich aus dem vorgegebenen Flächeninhalt: Bei der Betrachtung ist unmittelbar ersichtlich, dass es eine geeignetere Näherung an ein Quadrat gibt, denn die eine Seitenlänge x0 = 1 ist zu klein, die andere mit y0 = 9 zu groß. Um eine verbesserte Annäherung an die Länge einer Quadratseite zu erhalten, kann das arithmetische Mittel der Seitenlängen x0 und y0 dienen (Hier gibt es eine ganze Reihe von Möglichkeiten, das Verfahren zu verfeinern.): Die Länge der zweiten Seite dieses neuen Näherungs-Rechtecks ergibt sich wieder durch den vorgegebenen Flächeninhalt a:

3. Lösungsalgorithmus

	Anfangswert wie oben beschrieben auf 1 gesetzt und nachfolgend der Lösungsalgoithmus durchgespielt ist mit Sicherheit eine elegante Lösungsidee - das Verfahren und damit die Idee wird so zu sagen 1 : 1 in das Programmiersystem übertragen.
	naeherung:=1; naeherung:=(naeherung+basiwert/naeherung)/2;

4. Programmvorschläge

	Hannes Uhlig hat unser Vorschläge konsequent aufgegriffen und einschließlich der Problematik Oma und Katze ein Programm des Kaprekar-Algorithmus notiert, in welchem schon einige Kerngedanken eines sauberen - eben noch nicht objektorientierten Programmieirstils zusammenlaufen.
	procedure TForm1.Button1Click(Sender: TObject); var   i:integer;   tiefe:integer;{Näherungstiefe}   basiwert:longint;{ganzzahliger Ausgangswert}   naeherung:real;{aktuell ermittelter Näherungswert} begin   tiefe:=StrToInt(Edit4.Text);   naeherung:=1;{Ausgangswert per Definition}   basiwert:=StrToInt(Edit2.Text);   for i:=1 to tiefe do   begin{begin of for}     naeherung:=(naeherung+basiwert/naeherung)/2;   end;{end of for}   Edit5.Text:=FloatToStr(naeherung); end;
	die Lösung für drei Näherungsschritte kommt der 3 schon sehr nahe die Lösung für drei Näherungsschritte kommt der 3 schon sehr nahe die Lösung für drei Näherungsschritte kommt der 3 schon sehr nahe

5. Zusammenfassung

	Im folgenden der Versuch, das Heron-Verfahren grafisch darzustellen. Dabei, und dem Ziel, sich gedanklich fast 2000 Jahre in der Geschichte zurück zu versetzen, fällt auf, dass die Idee genial, aber einfach war. Mit nur einem Näherungsschritt bekomme ich definitiv einen Fehler, aber schon nach 3 Schritten eine beachtliche Genauigkeit und lande nach 5 einen rein rechnerischen Volltreffer dessen Ungenauigkeit ich vernachlässigen kann.
	Näherungsschritte nach Heron-Verfahren auch gern als CorelDraw 11.0-Datei Näherungsschritte nach Heron-Verfahren auch an dieser Stelle ger als CorelDraw 11.0-Datei Näherungsschritte nach Heron-Verfahren ebenso ger als CorelDraw 11.0-Datei
	der Wert bereits für die dritte Näherung beträgt: 302,352941176471 ...
	Heronverfahren für Kantenlänge 33 mm nach drei Näherungssschritten warum hier nicht  als CorelDraw 11.0-Datei
	das sind: 99,163912113551051628650991916466 %

6. Weiterführende Literatur

7. Links zum Thema

	Wie immer ist auch Wikipaedia keine Kopiervorlage, aber eine sehr gute Rubrik, um aus den dortigen Ideen eigene Gedanken zu entwickeln. Da das Verfahren einfach zu elegant ist, steht es noch als iteratives Programmierschema schlechthin, kaum also ein Informatikstudent, der nicht einmal programmierungstechnisch über Heron stolpert.
	http://de.wikipedia.org/wiki/Heronverfahren
	http://mathenexus.zum.de/html/analysis/numerische_verfahren/weiterfuehrendes/heron.htm
	http://www.herder-oberschule.de/madincea/aufg0009/heron.pdf
	http://www.mathe-schule.de/download/pdf/Mathematik/Aufgaben_Heron.pdf

8. Verwandte Themen

	Das Vorangestellte hilft wirtschaften, löst jedoch kein einziges Problem (allerdings ohne Beachtung der Worst-Case-Strategien wird man auch nicht erfolgreich Software entwickeln und/oder informatische Projekte realisieren können). Deshalb nunmehr das, was wirklich Arbeiten hilft.
	das 8-Dame-Problem des Cliquen-Problem Domino-Problem das Entscheidbarkeitsproblem das Erfüllbarkeitsproblem die Fibonacci-Zahlen das Flaggenproblem das Halteproblem das Hamilton-Problem das K-Farben-Problem der Kaprekar-Algorithmus die Magischen Quadrate das PASCAL'sche Dreiecksproblem das Philosophenproblem das Königsberger-Brückenproblem das Post'schen Korrespondenzproblem das Rundreiseproblem das Springer-Problem die Türme von Hanoi das Wortproblem das Wüstenfit-Problem das 153-Problem
	Worst-Case-Denken Algorithmentheorie Komplexität, Mächtigkeit und Aufwand Praktische Elementaralgorithmen Lösbarkeit und Problemlösungsstrategien Klassische algorithmisch lösbare Probleme Zufall und Computer Graphentheorie Petri-Netze
	Informationsbegriff Logo für die Signale Nachrichten Wissen Systembegriff Modellbegriff Simulation Denken und Sprache Zahlen, Daten und Datentypen Gegenläufigkeit und Verklemmung Pattern-Matching HORNER-Schema

zur Hauptseite

© Samuel-von-Pufendorf-Gymnasium Flöha

© Frank Rost am 10. Januar 2008