 |
Der wesentliche Unterschied
zu MPEG (Motion Picture Expert Group) ist, dass JPEG jedes Bild für sich
komprimiert, während MPEG darüber hinaus Kenntnisse früherer und späterer
Bilder einer Videosequenz ausnutzt, um eine noch höhere Datenreduktion zu
erreichen. Das hat Konsequenzen für die Bearbeitung von MPEG-Bildsequenzen.
Man kann dort nicht jedes einzelne Bild laden, wie es zum Beispiel zum
Schneiden von Videosequenzen notwendig ist, da die Informationen über den
aktuellen Bildinhalt über mehrere Bilder verteilt sind.
Obwohl JPEG für die Kompression von Standbildern gedacht war, ist der Stand
der Halbleiter-Technologie soweit, dass 30 Bilder und mehr pro Sekunde in
Echtzeit bearbeitet werden können, so dass Video mit JPEG realisiert werden
kann. |
 |
Die DCT ist einer Fouriertransformation
sehr ähnlich. Da man den Formeln ansieht, dass die zweidimensionale DCT
durch eine Hintereinanderreihung von eindimensionalen DCTs, zuerst in
x-Richtung und dann in y-Richtung, ausgeführt werden kann, soll der
Einfachheit halber hier die eindimensonale DCT betrachtet werden.
Der Helligkeitsverlauf innerhalb eines Ausschnitts von acht Pixeln einer
Zeile (zum Beispiel seien dies die Werte 1, 7, 53, 193, 156, 117, 87)
wird nach der Formel 4 in Bild 5 durch Überlagerung der acht
Grundfunktionen (wie in Bild 6 gezeigt) dargestellt. Der Anteil der
einzelnen Grundfunktionen an der Gesamtfunktion wird durch die
Vorfaktoren C(u) bestimmt. Diese Vorfaktoren werden auch als
DCT-Koeffizienten bezeichnet. Für ihre Berechnung dient die Formel 3.
Da x nur ganzzahlige Werte von 0 bis 7 annimmt, nehmen auch die acht
Funktionen (u läuft dabei von 0 bis 7) cos(((2*x +1)*u*Pi)/16) nur
sieben Werte an (Bild Funktionsgraphen). Feinere Bilddetails werden von
den höherfrequenten Grundfunktionen erfasst, die gröberen werden von den
niederfrequenten Grundfunktionen dargestellt. Die Größe der
Koeffizienten vor den Grundfunktionen geben an, wie groß der Anteil
dieser Funktionen an der Bildinformation ist. Anders ausgedrückt
bedeutet dies, dass die Helligkeitsinformation nach Frequenzen sortiert
wird.
Im zweidimensionalen Fall, wo diese Sortierung nicht nur in x-, sondern
auch in y-Richtung erfolgt, kommt man zu einer Anordnung der
Koeffizienten in Matrixform wie in Bild 7. Die Anordnung der
Koeffizienten in der Matrix ist so, dass links oben der DC-Koeffizient
steht, während nach rechts und unten hin die Koeffizienten der
höherfrequenten Grundfunktionen stehen. Der DC-Koeffizient gibt den
Gleichanteil im Helligkeitsfeld an.
Man kann davon ausgehen, dass in einem Pixelblock (2,24 x 2,24
Millimeter) die Helligkeit eher schwach veränderlich ist, für die
Farbkomponenten gilt dies besonders. Aus diesem Grunde sind in den Y-, U
und V-Matrizen die Werte voneinander abhängig. Kennt man in einer Zeile
die Elemente 0, 1, 2, 3, 5, 6, und 7, so kann Element 4 nicht total aus
dem Trend fallen. Andersherum gesagt bedeutet das, dass in der
Information über die sieben bekannten Pixel schon sehr viel Kenntnis
über Pixel Nummer 4 enthalten ist. Die Helligkeitswerte sind voneinander
abhängig. Man spricht von Inter-Pixel-Redundanz. Besonders die Werte
nächster Nachbarn sind stark von einander abhängig. Diese Abhängigkeit
machen sich die nachfolgenden Schritte zunutze, um den Datenumfang
drastisch zu reduzieren.
Bevor diese Schritte beschrieben werden, einige Worte zu der Frage, ob
der Prozess bis hierher schon verlustbehaftet ist. Die
Farbraumtransformation von RGB nach
YUV ist umkehrbar, das heißt, die RGB-Information ist erhalten
geblieben. Das 4:2:2-Subsampling ist jedoch verlustbehaftet, aber
unwesentlich für das menschliche Sehvermögen. Im Prinzip werden bei der
DCT Informationen über das Bild nicht vernichtet.
Lässt man x und y in Formel 1 die Werte 0 bis 7 annehmen, so erhält man
64 Gleichungen mit 64 Unbekannten. Dieses Gleichungssystem hat eine
Lösung, und das heißt, man kann die Ausgangswerte wieder zurückrechnen.
Die DCT ist umkehrbar, abgesehen von Fehlern, die durch
Rechenungenauigkeit und Rundungsfehler entstehen. Insbesondere darf von
der Fouriertransformation nicht die bekannte Vorstellung übernommen
werden, dass unendlich viele Grundfunktionen nötig sind, um sich einem
Kurvenverlauf anzunähern. Das stimmt nicht einmal dort für einen
gesampelten Signalverlauf. Die Qualität des invers transformierten
Bildes ist nur durch die Rechengenauigkeit bestimmt.
In den 8 x 8 Pixel großen YUV-Matrizen ist niemand in der Lage zu sagen,
welches Pixel wichtiger ist als das andere. Jedoch kann man über die
drei DCT-Koeffizientenmatrizen natürlicher Bilder die Aussage machen,
dass die Informationen in wenigen informationstragenden Koeffizienten,
und zwar in der linken oberen Ecke, konzentriert werden. Dass das so
ist, konnte letztlich nur durch Analysieren von vielen Fotos, Fernseh-
oder Videobildern bestätigt werden. Von den höherfrequenten Anteilen in
der rechten unteren Ecke weiß man sehr viel, nämlich dass sie zum
Beispiel vielfach Null oder sehr klein sind. Wenn das aber bekannt ist,
enthalten diese Koeffizienten nichts Neues, oder mit anderen Worten, sie
enthalten keine Information. Der Datenumfang hat sich gegenüber der
RGB-Darstellung allerdings bisher nicht reduziert. Statt einem
Datenvolumen von 3 x 64 x 8 Bit für die RGB-Werte braucht man anstatt
der 8-Bit-Werte für die DCT-Koeffizienten jetzt mehr Platz, egal, ob sie
als Real- oder Integerzahl gespeichert werden. Die DCT ist die
rechenintensivste Operation im gesamten JPEG-Algorithmus. Erst im
übernächsten Schritt, der Lauflängen- und Huffmann-Codierung, wird der
Lohn der Mühe kassiert. Das Basic-Programm im Listing zeigt die Schritte
bei der Berechnung. Es ist leicht auf den zweidimensionalen Fall zu
erweitern. |
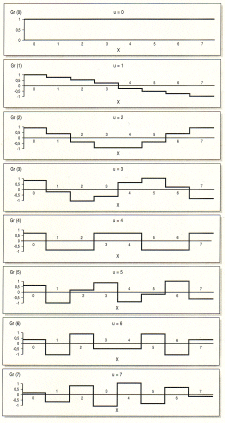
Jeder Funktionsverlauf mit
beliebigen Werten f(x) an den Stellen x=0 bis X=7 kann durch
Oberlagerung der acht Grundfunktionen der DCT Gr(u)=cos((2x+ 1)*u*Pi/
16), u=0 bis v=7 dargestellt werden in der Form f(x)=1 /2(C(0)/2
*Gr(0)+C(1)*Gr(1)+....*C(7)*Gr(7)). Die Werte für C(0)...C(7) werden
durch Formel 3 bestimmt. |
| Die Quantisierung
Während die DCT Abhängigkeiten in den YUV-Feldern reduziert, beseitigt
nun die Quantisierung Informationsanteile, die das menschliche Auge
ohnehin gar nicht oder nur sehr schlecht wahrnimmt. Die Quantisierung
erfolgt mit Hilfe einer so genannten psychovisuellen Gewichtsfunktion,
einer Matrix, die direkt für jeden einzelnen DCT-Koeffizienten die
Quantisierungsschrittweite enthält (Bild 8).
Diesen Matrizen ist unmittelbar anzusehen, dass die höherfrequenten
Details gröber, das heißt mit insgesamt weniger Schritten, dargestellt
werden. Bei der Farbinformation werden alle höherfrequenten
Koeffizienten kleiner als 99/2 nach der Rundungsvorschrift durch die 0
dargestellt. Die quantisierten DCT-Koeffizienten werden als
11-Bit-2er-Komplementzahlen mit Vorzeichen dargestellt. Die
Quantisierungsmatrizen sind von JPEG nicht vorgeschrieben. In Bild 9 ist
eine bei der Studionorm für digitales Fernsehen (CCIR601) gebräuchliche
Matrix angegeben. Da diese Matrix auf sehr viel Erfahrung beruht und nur
sehr aufwendig zu ermitteln ist, wird sie auch von anderen Normen
benutzt.
Die Quantisierung bewirkt zweierlei. Erstens nehmen die Koeffizienten
nicht mehr alle Werte zwischen -1023 und +1023 an, sondern zwischen
-1023/Schrittweite und +1023/Schrittweite. Bei einer Schrittweite von 99
wird der Bereich also zwischen -11 und +11 beschränkt. Zweitens, dass
insbesondere viele der ohnehin schon kleinen Koeffizienten rechts unten
durch die Quantisierung zu Null werden.
Vor allem an dieser Stelle, bei den Quantisierungskoeffizienten, kann
der Anwender in den Vorgang eingreifen, um den Kompressionsfaktor, und
damit auch die Qualität des Verfahrens, einzustellen. Die einfachste
Methode ist, jeden der Quantisierungskoeffizienten mit demselben Faktor
durchzumultiplizieren und damit die Abstufungen zu verändern. Die
Quantisierung ist der eigentliche verlustbehaftete Prozess im
JPEG-Algorithmus.
Im JPEG-Dokument wird ausdrücklich angemerkt, dass bei Verfeinerung der
Quantisierungsintervalle um den Faktor 2 das dekomprimierte Bild vom
Original nicht zu unterscheiden ist.
|
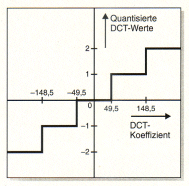
Bei einer
Quantisierungschrittweite von wie hier angenommen 99 werden alle
DCT-Koeffizienten zwischen -49,5 und 49 durch die 0 dargestellt. Die
1 steht für alle Werte zwischen 49,5 und 148,5 und so weiter. |
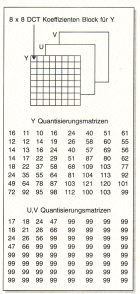
Die
Quantisierungsschrittweiten stehen in Quantisierungsmatrizen, auch
psycho visuelle Gewichtsfunktionen genannt. Jeder DCT-Koeffizient
wird mit der Schrittweite quantisiert, die an der entsprechenden
Stelle der Quantisierungsmatrizen steht. Bei der Chrominanz fällt
besonders auf, daß nur sehe wenige DCT-Elemente mit feiner Stufung
quantisiert werden, die überwiegende Mehr zahl wie im obigen
Beispiel mit einer Schrittweite von 99. |
|
|

Zweidimensionale DCT.
Dargestellt ist ein Übergang von hell nach dunkel (Luminanzanteil).
Die erste Matrix enthält die 64 Luminanzwerte. Die nächste Matrix
zeigt, dass die DCT in diesem Fall nur sehr wenige von 0
verschiedene DCT-Koeffizienten ergibt. Die letzte Matrix zeigt den
Effekt von Quantisierung und anschließender Dequantisierung auf die
DCT-Koeffizienten. Es werden weitere Null-Werte erzeugt. |
 |
| |
|
|
|
 |
Um eine hohe Datenreduktion zu erreichen,
arbeitet das Verfahren so, dass aus den gepackten Daten die
Originaldatei (das Originalbild) nicht vollständig rekonstruiert werden
kann. Es werden bei der Kompression bewusst unwichtige Informationen
verworfen.
Da JPEG häufig für Bilddaten genutzt wird, die auf einem Monitor
dargestellt werden sollen, lassen sich die Überlegungen, die zu diesem
Verfahren führten, am besten an dem Monitor-Bildaufbau erläutern.
Ausgangspunkt ist ein zeilenweise abgetastetes Bild, das durch die
Farbanteile für Rot, Grün und Blau (RGB) dargestellt wird. Jeder
Farbanteil wird mit einer Auflösung von 8 Bit digitalisiert. Pro Pixel
werden also 24 Bit benötigt. Die RGB-Informationen bestimmen die
Energie, die verwendet wird, um auf dem Monitor nah beieinanderliegende
Phosphorpunkte in den Farben Rot, Grün und Blau zum Leuchten anzuregen.
Für die Bearbeitung nach JPEG ist die Zeilendarstellung in ein
Blockformat von 8 x 8 Pixeln umzusetzen (Bild rechts).
Die Bearbeitungsschritte beim Baseline JPEG QPEG-Basisprozess), wie sie
auch im JPEG-Prozessor „CL550" von C-Cube durchgeführt werden, sind im
nächsten Bild dargestellt. Die folgenden Erläuterungen beschreiben den
Prozess der Datenverdichtung (Encoding), der umgekehrte Prozess verläuft
entsprechend. |
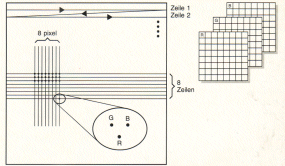
Videobilder sind zeilenweise aufgebaut. Die
einzelnen Bildpunkte oder Pixel (Picture Elements) bestehen aus Punkten
roten und grünen und blauen Phosphors. Die RGB-Signale bestimmen die
Heiligkeit, mit der die Punkte leuchten. Für JPEG muss das Zeilenformat
in ein Blockformat von 8 x 8 Pixel überführt werden. Pro 8 x 8-Pixelfeld
werden je eine Matrix für die Rot-, Grün- und Blau-Information benötigt. |
| Änderung
des Farbmodells Obwohl das zu verwendende Farbmodell
nicht Gegenstand der JPEG-Norm ist, werden die besten Ergebnisse
erzielt, wenn das vom Farbfernsehen bekannte YUV-Modell gewählt wird.
Die Helligkeit (Luminanz) wird dabei mit Y bezeichnet, die
Farbinformation (Chrominanz) ist in U und V enthalten (Bild 3).
Es gibt zwei Gründe, weswegen die YUV-Darstellung für die
Bilddatenkompression so gut geeignet ist. Erstens kann das menschliche
Auge örtliche Helligkeitsunterschiede sehr viel besser auflösen und
damit unterscheiden als Farbänderungen. Zweitens sind die Helligkeits-
und die Farbinformationen bei YUV nicht voneinander abhängig. So ändert
sich der Farbton eines Bildes oder Bildausschnittes nicht, wenn die
Helligkeit geändert wird. Daher können die Informationen für Helligkeit
und Farbe unabhängig voneinander und vor allem mit unterschiedlichen
Kompressionsverhältnissen reduziert werden. Die Farbkomponenten
erreichen in der Praxis sehr viel größere Datenverdichtungen als die
Y-Anteile. Vom Schwarzweiß-Fernsehen, wo lediglich die Y-Komponente
dargestellt wird, ist allgemein bekannt, dass im Helligkeitssignal
bereits soviel Information enthalten ist, dass diese Darstellung vom
menschlichen Auge sehr gut verarbeitet wird.
Für die Verwendung des YUV-Modells müssen die vorhandenen RGB-Werte
umgerechnet werden. Die Transformation von RGB nach YUV erfolgt durch
eine im Bild 4 angegebene Matrizenmultiplikation. Die YUV-Komponenten
ergeben sich als gewichtete Summe aus den RGB-Komponenten (Y = 0,299*R +
0,587*G + 0,114*B, U = -0,169*R + -0,3316*G + 0,5*B, V = 0.5*R +
-0,4186*G + -0,0813*B). Der Helligkeitseindruck (Y) wird stärker von der
Grünkomponente als von der Rot- und der Blaukomponente bestimmt, nämlich
im Verhältnis 0,587 zu 0,299 und 0,114. Damit wird der höheren
Empfindlichkeit des menschlichen Auges für Grün Rechnung getragen.
Eine erste Reduktion der Datenmenge kann jetzt vor dem eigentlichen
JPEG-Prozess vorgenommen werden. Weil nämlich das Auge nicht so viele
Farbdetails unterscheiden kann wie Helligkeitsdetails, ist es nicht
notwendig, beide mit derselben Genauigkeit abzutasten. Daher wird ein so
genanntes 4:2:2-Subsampling (Unterabtastung) verwendet. Für vier
Helligkeitswerte in einer Zeile werden je zwei Farbwerte U und V
verwendet. Das heißt, dass für die Ermittlung der Farbwerte nur jedes
zweite Pixel für die eigentliche Bildkompression verwendet wird. Indem
mit einem Verhältnis von 4:2:2 weitergearbeitet wird, anstatt mit 4:4:4,
ist der Kompressionsgewinn 3:2. An dieser Stelle wird auf unterster
Ebene nicht benötigte Information ignoriert.
Diskrete Cosinus-Transformation Die YUV-Werte, die zunächst durch
Subtraktion von 128 in den Bereich zwischen -128 und +127 gebracht
werden, sind Ausgangspunkt des eigentlichen JPEG-Algorithmus.
Der erste Schritt ist die zweidimensionale Diskrete
Cosinus-Transformation (DCT). Für die DCT werden Blöcke von 8 x 8 Pixeln
aus einem Bild betrachtet, genauer gesagt, drei Felder der Größe 8 x 8
jeweils für die Werte von Y, U, und V.
Bei voller Ausnutzung der Auflösung eines üblichen 14-Zoll-Monitors mit
1024 x 768 Pixeln und einem Pixelabstand von 0,28 Millimetern haben die
Quadrate eine Kantenlänge von 2,24 Millimetern. Jedes dieser Felder wird
getrennt bearbeitet. Bei JPEG-Hardware hoher Leistungsfähigkeit, zum
Beispiel für die Komprimierung von Videobildern in Echtzeit, muss ein so
genannter „Strip-Buffer" für Streifen von acht Zeilen vorgesehen sein,
aus dem der JPEG-Baustein die Information blockweise entnimmt. Bei
reiner Standbild-Kompression kann die Aufbereitung des zeilenweise
aufgebauten Bildes in 8x8-Blöcke auch durch Software erfolgen.
Die in nebenstehendem Bild aufgeführten Formeln für die DCT, auch
„Forward DCT" genannt (FDCT), und die „Inverse DCT" (IDCT) sind einander
so ähnlich, dass sich jede Hardware für die Berechnung der
Transformation leicht so auslegen lässt, dass sie beide
Transformationsrichtungen ausführen kann. Daher ist beispielsweise der
CL550 ein so genannter CODEC (Coder/Decoder), der genauso schnell
komprimieren wie dekomprimieren kann. Hierin besteht ein weiterer
Unterschied zu MPEG, wo die Kompression der Bildinformation sehr viel
aufwendiger ist, als die anschließende Zurückgewinnung.
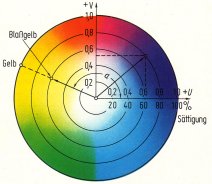
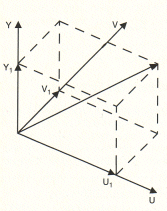
Der Farbvektor wird durch die Yl
-, U 1und Vl-Komponenten dargestellt. Der Farbton wird von U und V
bestimmt, die Helligkeit von Y. Die Helligkeit enthält mehr
Informationen als die Farbton-Komponenten und kann geändert werden, ohne
den Farbton zu beeinflussen. Der Zusammenhang zwischen U, V und der
jeweiligen Farbe geht aus dem Farbdiagramm hervor. |
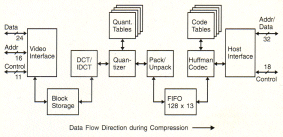
Blockdiagramm des CL550 von C-Cube.
Der Datenflug bei der Kompression geht von links nach rechts. |
|
 |
|

Umrechnungsmatrix von RGB nach YUV |
|

Formeln der ein- und zweidimensionalen
DCT |
|
 |
| Die
Zick-Zack-Aufreihung Im nächsten Arbeitsschritt werden
die ACElemente der quantisierten Koeffizientenmatrix in einer
Zick-Zack-Folge aufgereiht (Bild rechts).
Die DC-Koeffizienten werden in anderer Weise behandelt als die
AC-Koeffizienten. Es wird bei ihnen die Differenz zum vorhergehenden
Block codiert. Wichtiger ist jedoch das Verfahren für die 63
AC-Koeffizienten.
Es entsteht eine Kette aus 63 Elementen (ZickZack(1)...ZickZack(63)).
Durch diese Abtastung der Matrix entstehen - vor allem zum Ende hin -
möglichst viele Abschnitte aufeinanderfolgender Nullen. Nach diesem
Schritt beginnt die Verringerung des Datenumfangs nach Lauflängen- und
HuffmannCodierung.
Die Lauflängen-Codierung
Die Folge der 63 Zick-Zack-geordneten Koeffizienten wird
beispielsweise im CL550 in der „Zero-Pack-Unit" in eine Form überführt,
bei der nur Koeffizienten ungleich Null in der Form RS = RRRRSSSS
dargestellt werden. Jedes R und S steht dabei für einen binären
Zahlenwert. Das Zeichen R steht für die Abkürzung Runlength (Lauflänge),
S für Size (Größe).
Das Verfahren ist darauf abgestellt, eine effektive Codierung von
Sub-Strings aufeinanderfolgender Nullen zu finden. Die Zeichen RRRR
stehen für eine 4-Bit-Runlength,
die angibt, wieviele Nullen vor dem codierten Koeffizienten stehen. Ist
in der ZickZack-Folge beispielsweise der 46. Koeffizient ungleich Null,
und sind alle Werte von ZickZack(47)...ZickZack(53)=0, und ist
ZickZack(54)=3, so wird der 54. Koeffizient (ZickZack(54)) mit RRRR=0111
codiert, da vor ihm sieben (binär 0111) Nullen stehen. Für
ZickZack(54)=3 ist SSSS=0010, wie aus folgender Liste hervorgeht:
SSSS AC-Koeffizient 1 1,1
2 -3...-2,2...3
3 -7...-4,4...7 USW.
10 -1023...-512,512...1023 Die SSSS-Folge bestimmt die höherwertigen
Bits, der niederwertigen Bits werden
an das RS-Symbol uncodiert angehängt. Folgen mit mehr als 15 Nullen
werden durch RS= 11110000, das als eine Folge von 16 Nullen
interpretiert wird, unterteilt.
Der wichtige Sonderfall, dass ab einem bestimmten Koeffizienten nur noch
Null-Koeffizienten folgen, wird durch das EOB-Zeichen (End of Block,
RS=00000000) dargestellt. Der Decoder kann dann die restlichen Zeichen
mit Nullkoeffizienten auf 63 ergänzen. Damit lassen sich unter Umständen
sehr viele Koeffizienten mit einem Zeichen darstellen, das heißt, es
wird eine sehr hohe Datenverdichtung erzielt. Ergebnis dieses Schrittes
ist eine Bitfolge, die aus den RS-Symbolen mit angehängten
niederwertigen Bits besteht und durch das EOBZeichen beendet wird.
Die Huffmann-Codierung
Im nächsten und letzten Schritt werden die RS-Elemente der Folge
sowie die EOB-Zeichen Huffmann-codiert. Die niederwertigen Bits werden
uncodiert belassen. Huffmann-Codes nutzen statistische Eigenschaften der
zu codierenden Information aus, in diesem Fall der RS-Werte, um Daten zu
reduzieren. Betrachtet wird die Häufigkeit beziehungsweise die
Wahrscheinlichkeit des Auftretens eines bestimmten RS-Wertes. Dann wird
den selten auftretenden RS-Werten ein langes Codewort zugeordnet,
während häufigen ein kurzer Code zugeordnet wird (Bild 11). Soll ein
optimales Ergebnis erzielt werden, muss ein Huffmann-Code Verwendung
finden, der der Statistik eines speziellen Bildes oder einer speziellen
Gruppe von Bildern angemessen ist. Die Codierung erfolgt dann in zwei
Schritten. Im ersten Durchlauf werden die Daten statistisch ausgewertet.
Es wird abgezählt, wie oft eine bestimmte Kombination von 0-Lauflängen
und der Koeffizientengröße RRRRSSSS auftritt. Daraus wird ein
Huffmann-Code ermittelt, der zur Codierung herangezogen wird. Alternativ
kann eine Standardtabelle verwendet werden. Hier ein kleiner Ausschnitt:
RRRR SSSS Huffmann-Code-Word
0000 0000 1010 (EOB)
0000 0001 00
0000 0010 01
0000 0011 100
0000 0100 1011
0000 0101 11010
0000 0110 1111000
0000 0111 11111000 0000 1000 1111110110 0000 1001 1111111110000010 0000
1010 1111111110000011
Die Huffmann-Codierung ist ein verlustfreier Prozess. Durch
Verwendung unterschiedlicher Huffmann-Tabellen kann wiederum der
Kompressionsfaktor beeinflusst werden. Man kann sich leicht vorstellen,
dass für Bilder, die nur Text enthalten, wie zum Beispiel eine
eingescannte Schreibmaschinenseite, andere Huffmann-Tabellen angemessen
sind, als für reine Videobilder.
Leistungsfähigkeit des Verfahrens Ungeübte Beobachter können Bilder, die
um den Faktor 25 komprimiert wurden, üblicherweise nicht vom Original
unter
scheiden (Bilder 12 bis 17). Ein Pixel wird in diesem Fall durch 1 Bit
beschrieben, statt durch 24 Bit für die RGB-Werte.
Ein Windows-Programm, das den DCT-Algorithmus für verschiedene
Helligkeitsmuster demonstriert, wurde uns von der Firma Metronik (Distributor
von C-Cube), 8025 Unterhaching, zur Verfügung gestellt. Es ist in Visual
Basic für Windows 1.0 geschrieben. Das Programm und der Sourcecode sind
auf der Paperdisk in dieser Ausgabe enthalten sowie als Servicediskette
mcSoftedition 6/93 über den Verlag zu beziehen.
Jürgen Buck/kw |
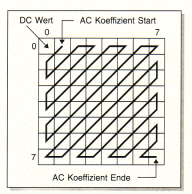
Zur Erzeugung einer Kette mit
vielen aufeinanderfolgenden Nullen wird die Matrix der DCT-Koeffizienten
im Zick-Zack-Ver fahren abgetastet. |
|
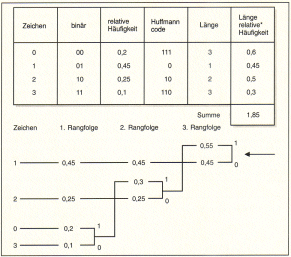
Aufbau eines Huffmann-Codes. Für
die Zeichen 0, 1, 2, 3 mit der relativen Auftrittshäufigkeit 0,2; 0,45;
0,25 und 0,1 kann ein Huffmann-Code nach dem obigen Schema ermittelt
werden:
1. Die Zeichen werden nach ihrer Häufigkeit geordnet, wie unter der
ersten Rangfolge im Diagramm.
2. Die Häufigkeiten der unteren Zeichen werden addiert, und mit dieser
wird eine neue Rangfolge gebildet.
3. Dieser Vorgang wird so lange wiederholt, bis es nicht mehr geht.
4. Dort, wo wie unter Punkt 2 eine Summe der Wahrscheinlichkeiten
gebildet wird, wird an den oberen Summanden eine 1 geschrieben und an
den unteren eine 0. Der Huffman-Code, eines Zeichens ergibt sich, indem
man das in der Zeichnung gezeigte Schema von rechts zu diesem Zeichen
hin durchläuft und dabei alle Einsen und Nullen hintereinander
aufschreibt. Huffman-Codes können ohne Trennzeichen hintereinander
aufgereiht werden, weil kein Code als Substring am Beginn eines anderen
auftritt.
In Beispiel braucht der Huffman-Code im Mittel 1,85 Bit pro Zeichen, im
Vergleich zu 2 Bit in der Binärdarstellung. |
|
 |

Zwei Beispiele, wie gut der
JPEG-Algorithmus arbeitet. Sie wurden so gewählt, dass ein Bildverlust
sichtbar ist. Es sind Bilder mit 256 Farben. In der ersten Reihe sind die
Originalbilder zu sehen. In der zweiten Reihe wurden die Bilddaten auf die
Hälfte reduziert. In der dritten Reihe umfassen die komprimierten Daten
gerade einmal fünf Prozent der Originalgröße. |
 |
|