Huffman-Codierung

Die Idee
Die Huffman-Kodierung ist ein Verfahren, dass eine Codierung von Eingabewörtern
gleicher Länge mit Codes unterschiedlicher Länge unter Berücksichtigung
der Fano-Bedingung ermöglicht. Dabei hat der
Professor der Informatik David A. Huffman Im Jahre 1952 den Durchbruch
erzielt. Er ermöglichte es die Baumstruktur soweit zu verändern, dass
der Baum und der entstehende Code immer optimal ist.
Der optimale Baum - aber wie? :
Die Grundidee der Huffman-Kodierung ist die Sortierung der Eingabewörter
nach ihrer Häufigkeit innerhalb der Eingabe. Unter Eingabewörtern
versteht man meist Buchstaben, obwohl die Kodierung auch mit jeglichen
anderen Daten machbar ist. Das genaue Funktionsprinzip soll anhand mehrer
(Text-)Beispiele erklärt
werden.
erstes Beispiel: AABAACDAAEABACD
Als erstes versuchen wir die Zeichenkette AABAACDAAEABACD möglichst
platzsparend zu kodieren. Zuerst muss man die Häufigkeiten und die
Wahrscheinlichkeiten aller Zeichen des Eingabestrings ermitteln:
| Zeichen |
Häufigkeit in der Eingabe |
Wahrscheinlichkeit de Zeichens |
| A |
8 |
8/15 |
| B |
2 |
2/15 |
| C |
2 |
2/15 |
| D |
2 |
2/15 |
| E |
1 |
1/15 |
Nun werden die zwei Eingabezeichen unter einem Knoten zusammengefasst,
die die kleinste Summe der Wahrscheinlichkeiten ergeben: In diesem Beispiel
wären das D und E. Diese bezeichnen wir ganz einfach mit Z und es
erhät
die Häufigkeit 3. Diesen Schritt wiederholen wir und fassen
jetzt die Häufigkeiten von B und C zusammen, da diese in der Summe
die kleinste Häufigkeit ergeben. Die Summe bezeichnen wir einfach
mit Y. Das wird solange wiederholt, bis nur noch ein Knoten übrig
ist. An dieser Abbildung wird es vielleicht noch deutlicher:
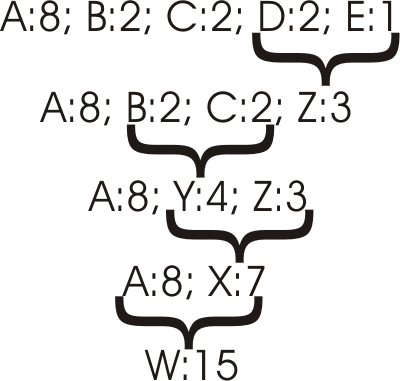
Wer sich jetzt nicht vorstellen kan wie man daraus einen Codebaum erstellt
der bekommt ihn hier:
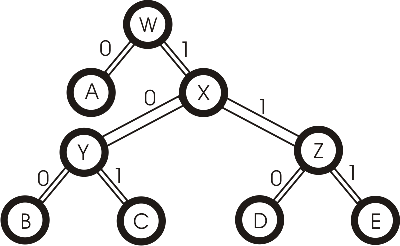
Aus diesem Baum kann man nun das Wörterbuch aufbauen. Das würde lauten:
A-0; B-100; C-101; D-110; E-111. Wie sich erkennen lässt erfüllt dieser Code
die Fano-Bedingung.
Anhand diesem Wörterbuch kann man nun die Zeichenfolge AABAACDAAEABACD kodieren,
es ergibt sich: 001000010111000
11101000101110, also eine Bitfolge mit der Länge 29. Diese Kodierung ist
die kürzeste mögliche. Dieser Sachverhalt wurde mathematisch bewiesen.
Um die Zeichenfolge wieder entshöüsseln zu können muss das Wörterbuch natürlich
mit übertragen werden.
zweites Beispiel: Mississippi
Dieses Beispiel möchte ich kürzer fassen: Als erstes muss man die Häufigkeiten
ermitteln:
| Zeichen |
Häufigkeit in der Eingabe |
Wahrscheinlichkeit de Zeichens |
| M |
1 |
1/11 |
| I |
4 |
4/11 |
| S |
4 |
4/11 |
| P |
2 |
2/11 |
Zusammenfassung zu Knoten:

Erzeugung des Baumes:
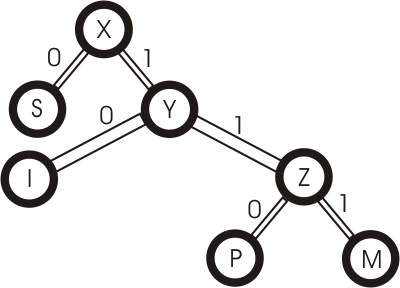
Wörterbuch: S-0; I-10; P-110; M-111
Kodierter Eingabestring: 111100010001011011010 (21 Bit)
Zurückübersetzung:
Die Zurückübersetzung ist eigentlich relativ einfach - entweder hat man
den Baum oder das Wörterbuch. Hat man den Baum beginnt man an der Wurzel
und geht bei einer 0 nach links und bei einer 1 nch rechts bis man bei
einem Buchstaben abngelangt ist. Da die Codes die Fano-Bedingung erfüllen
ducht man beim Nachschlagen im Wörterbuch (dieses sollte nach Code sortiert
sein) einfach nach der Zeichenkette die passt.





 Alle
Mandelbrot-Grafiken bereitgestellt von
André Neubert Klassenstufe 12,
Alle
Mandelbrot-Grafiken bereitgestellt von
André Neubert Klassenstufe 12,