Logikschaltung
Kanonische Normalform
Die kanonische Normalfrom ist die Ausgangsform für
die Logikschaltung. Am besten zu erklären ist diese
an einem Beispiel.
- 5 Eingänge=X0, X1, X2, X3, X4
- 2 Ausgänge=Y0, Y1
Die Eingänge können dabei 0 oder 1 annehmen.
Da es unter anderem Wiederholungen geben kann,
gibt es insgesamt 5*5*5*5*5=2^5=32 Möglichkeiten
Darstellung aller Eingangs- und Ausgangsmöglichkeiten:
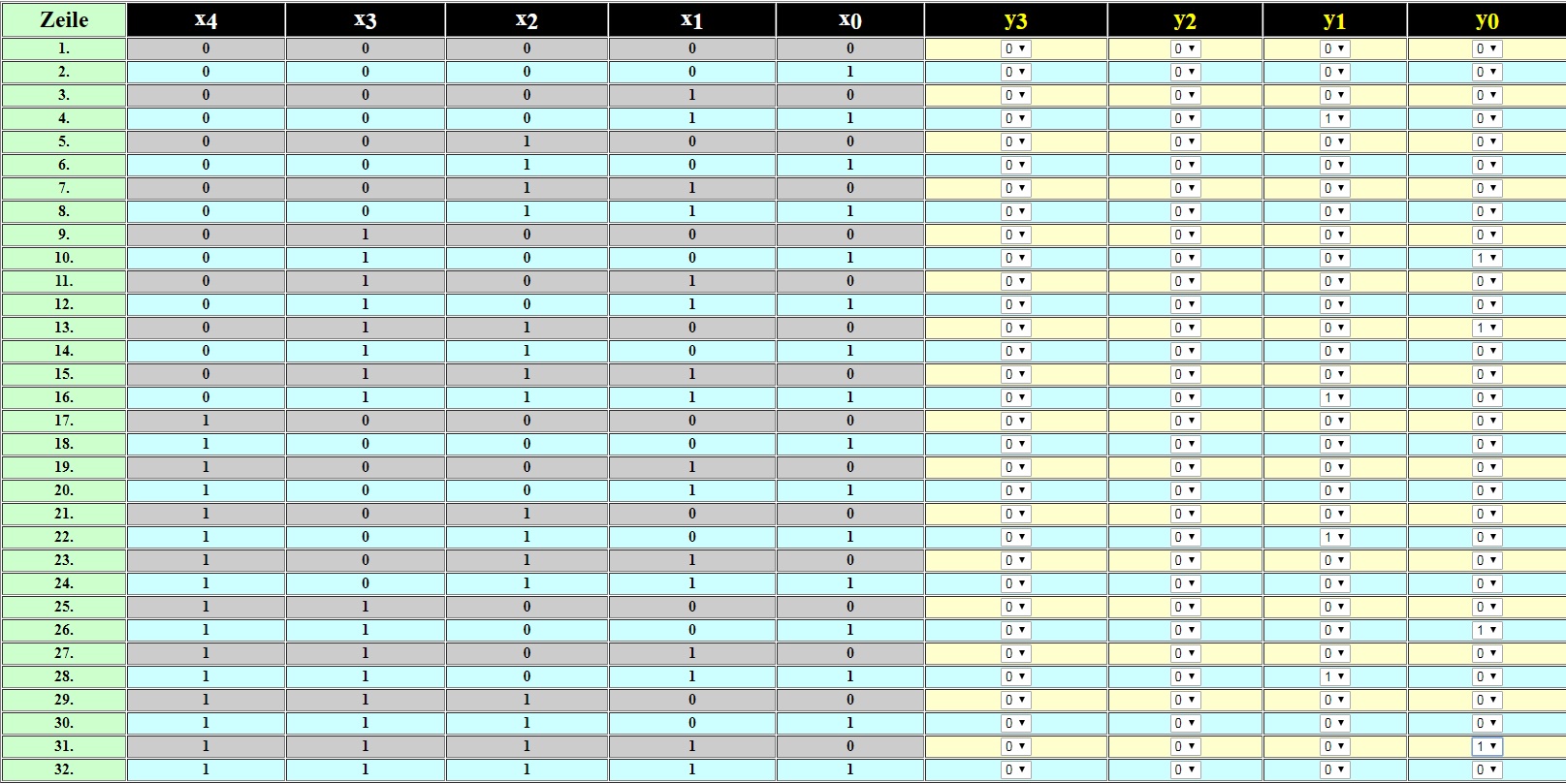 Im dargestellten Beispiel gibt es für jeden Ausgang nur 4 logische Einsen.
In den anderen 28 Fällen ergeben sich je Ausgang logische Nullen.
Einzelne Betrachtung der Ausgänge:
Formel Y=0 :
Im dargestellten Beispiel gibt es für jeden Ausgang nur 4 logische Einsen.
In den anderen 28 Fällen ergeben sich je Ausgang logische Nullen.
Einzelne Betrachtung der Ausgänge:
Formel Y=0 :
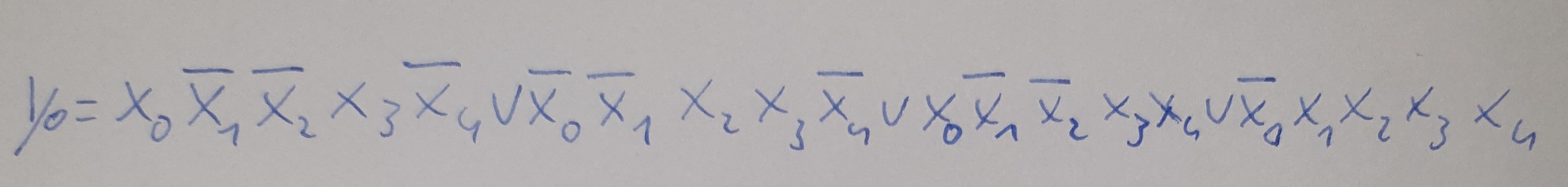 Formel Y=1 :
Formel Y=1 :
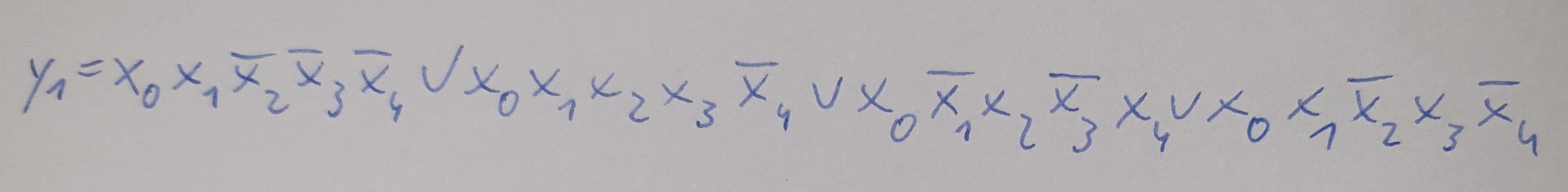
Normalform als Logikschaltung in ProfiLab:
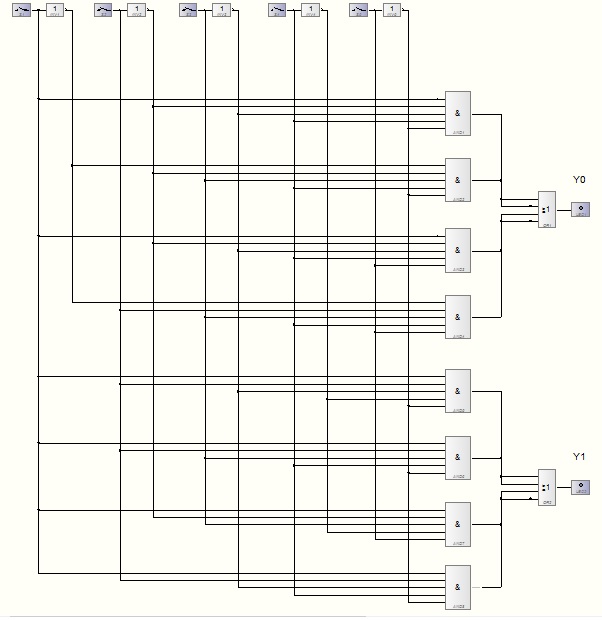 Beispiel dafür dass ein Fall für Y0=1 eintritt:
Beispiel dafür dass ein Fall für Y0=1 eintritt:
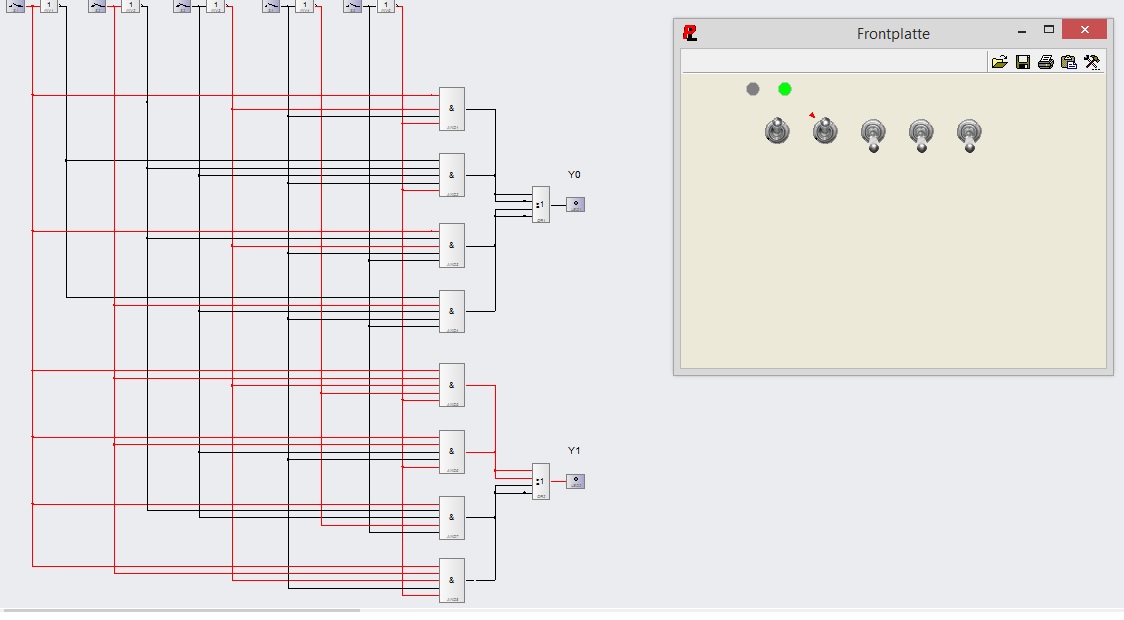
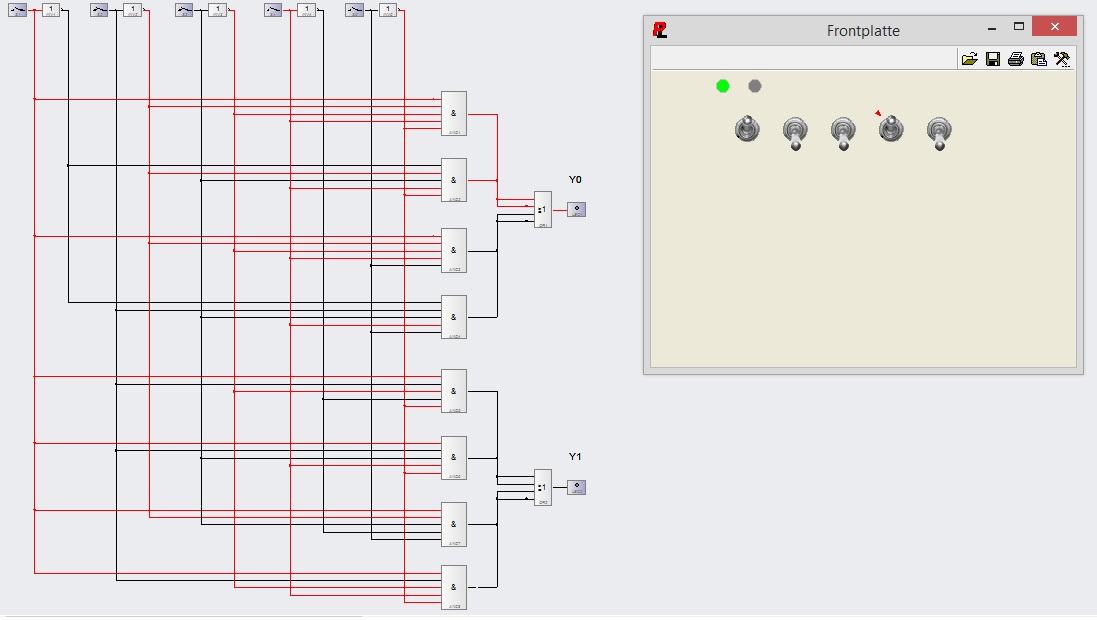 Beispiel dafür dass ein Fall für Y1=1 eintritt:
Beispiel dafür dass ein Fall für Y1=1 eintritt:
Karnaugh-Form
Die Karnaugh Form unterscheidet sich in der Schreibweise.
Sie dient lediglich der Vereinfachung.
Um die Karnaugh-Form zu ermitteln nutzt man eine Logiktabelle.
In diese setzt man dann die Y0 und Y1 Schreibweise ein :
Für Y0=1:
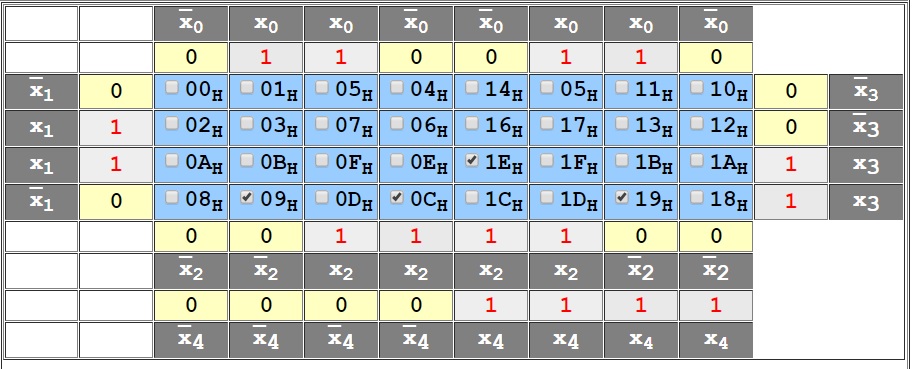 Für Y1=1:
Für Y1=1:
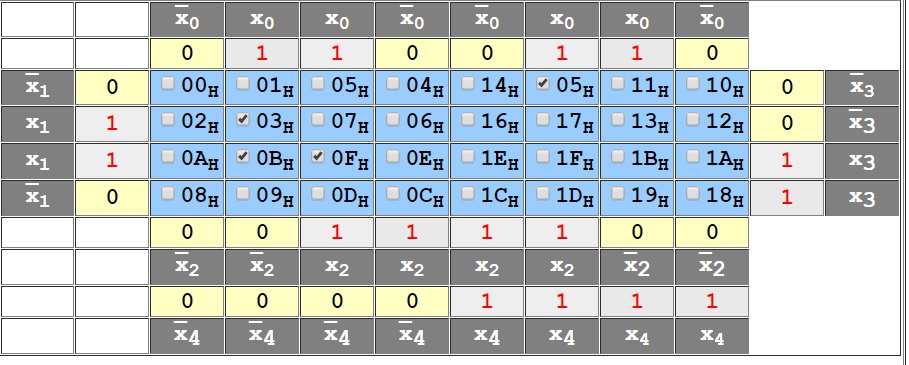 In meinem Fall vereinfacht sich nur die Y=1 Formel vereinfacht. Neue Formel:
In meinem Fall vereinfacht sich nur die Y=1 Formel vereinfacht. Neue Formel:
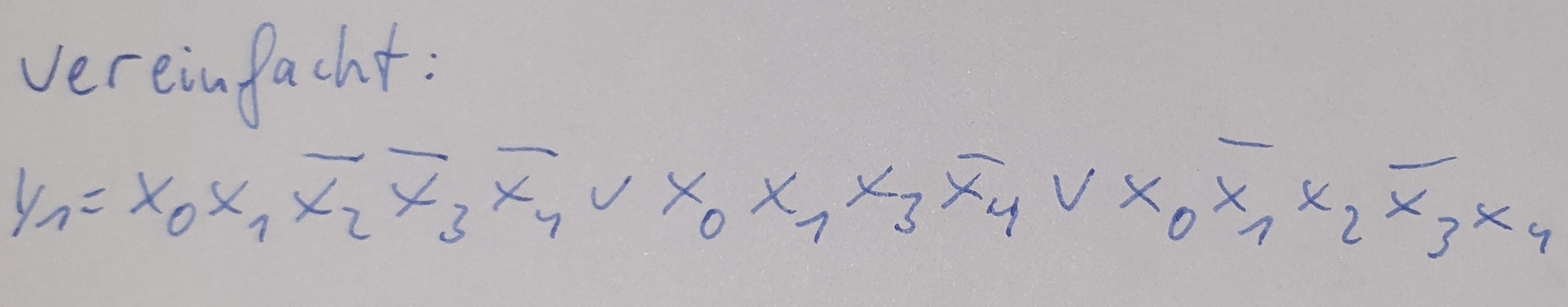 Die Logikschaltung sieht nun folgendermaßen aus:
Die Logikschaltung sieht nun folgendermaßen aus:
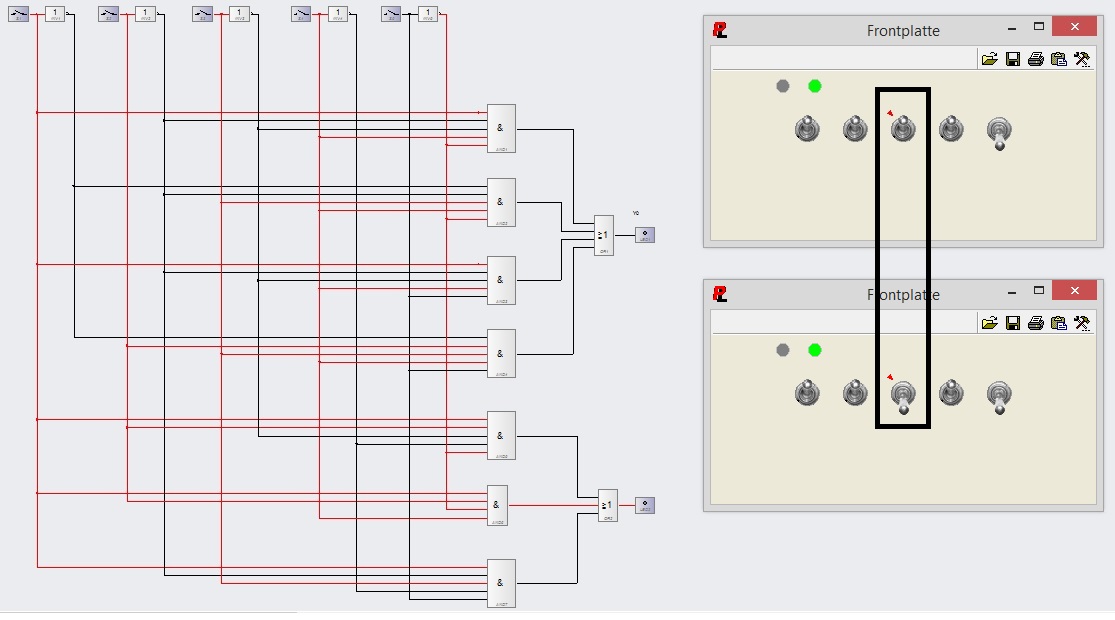 Man kann also erkennen dass Y1=1 unabhängig von X2 ist.
Deshalb leuchtet die LED in beiden Fällen.
Man kann also erkennen dass Y1=1 unabhängig von X2 ist.
Deshalb leuchtet die LED in beiden Fällen.
Logikschaltung
Folgende Bilder zeigen nun alle 32 möglichen Zustände.
Dabei ist festzustellen dass die LEDs nur bei der
Vorraussetzung Y0=1 und Y1=1 leuchten. Dieser Zustand
wird nur erreicht wenn die oben beschriebene Formel
erfüllt wird.
Bild 1
 Bild 2
Bild 2
 Bild 3
Bild 3
 Bild 4
Y1=1
Bild 4
Y1=1
 Bild 5
Bild 5
 Bild 6
Bild 6
 Bild 7
Bild 7
 Bild 8
Bild 8
 Bild 9
Bild 9
 Bild 10
Y0=1
Bild 10
Y0=1
 Bild 11
Bild 11
 Bild 12
Y1=1
Bild 12
Y1=1
 Bild 13
Y0=1
Bild 13
Y0=1
 Bild 14
Bild 14
 Bild 15
Bild 15
 Bild 16
Y1=1
Bild 16
Y1=1
 Bild 17
Bild 17
 Bild 18
Bild 18
 Bild 19
Bild 19
 Bild 20
Bild 20
 Bild 21
Bild 21
 Bild 22
Y1=1
Bild 22
Y1=1
 Bild 23
Bild 23
 Bild 24
Bild 24
 Bild 25
Bild 25
 Bild 26
Y0=1
Bild 26
Y0=1
 Bild 27
Bild 27
 Bild 28
Bild 28
 Bild 29
Bild 29
 Bild 30
Bild 30
 Bild 31
Y0=1
Bild 31
Y0=1
 Bild 32
Bild 32
 Zum Seitenanfang
Zurück
Home
Zum Seitenanfang
Zurück
Home
 Im dargestellten Beispiel gibt es für jeden Ausgang nur 4 logische Einsen.
In den anderen 28 Fällen ergeben sich je Ausgang logische Nullen.
Einzelne Betrachtung der Ausgänge:
Formel Y=0 :
Im dargestellten Beispiel gibt es für jeden Ausgang nur 4 logische Einsen.
In den anderen 28 Fällen ergeben sich je Ausgang logische Nullen.
Einzelne Betrachtung der Ausgänge:
Formel Y=0 :
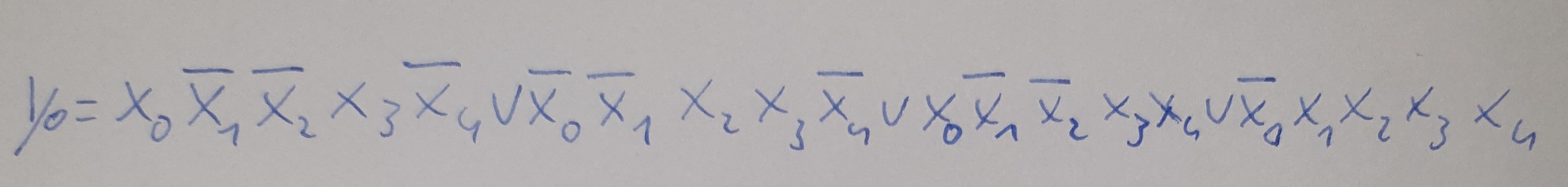 Formel Y=1 :
Formel Y=1 :
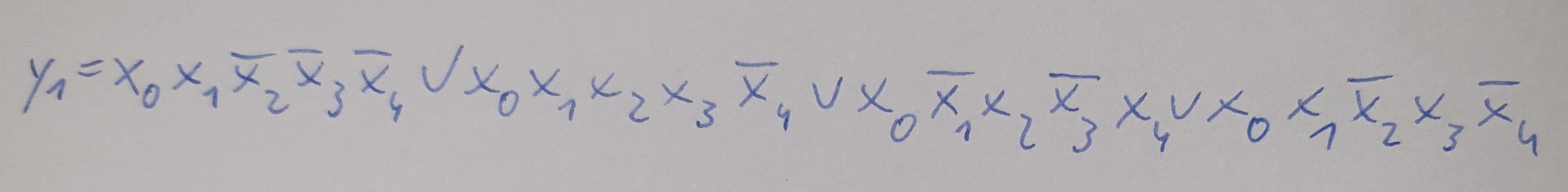
 Beispiel dafür dass ein Fall für Y0=1 eintritt:
Beispiel dafür dass ein Fall für Y0=1 eintritt:
 Beispiel dafür dass ein Fall für Y1=1 eintritt:
Beispiel dafür dass ein Fall für Y1=1 eintritt:

 Für Y1=1:
Für Y1=1:
 In meinem Fall vereinfacht sich nur die Y=1 Formel vereinfacht. Neue Formel:
In meinem Fall vereinfacht sich nur die Y=1 Formel vereinfacht. Neue Formel:
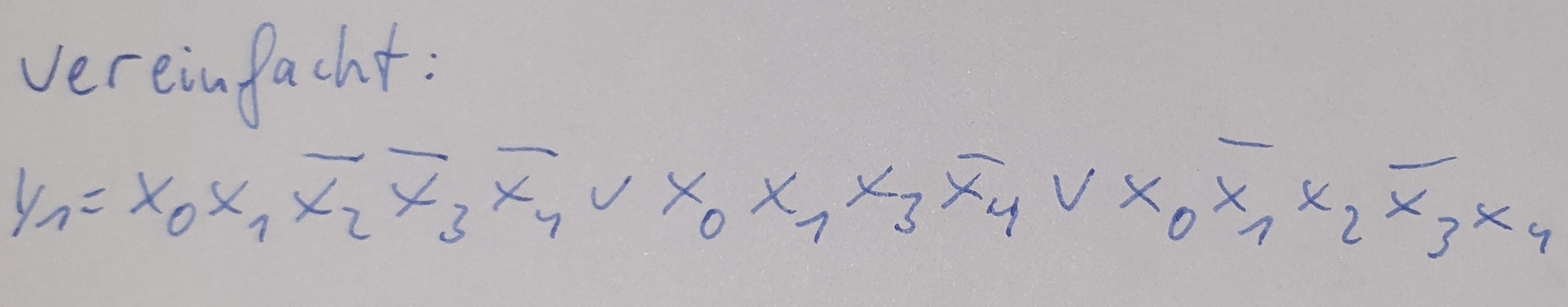 Die Logikschaltung sieht nun folgendermaßen aus:
Die Logikschaltung sieht nun folgendermaßen aus:
 Man kann also erkennen dass Y1=1 unabhängig von X2 ist.
Deshalb leuchtet die LED in beiden Fällen.
Man kann also erkennen dass Y1=1 unabhängig von X2 ist.
Deshalb leuchtet die LED in beiden Fällen.
 Bild 2
Bild 2
 Bild 3
Bild 3
 Bild 4
Y1=1
Bild 4
Y1=1
 Bild 5
Bild 5
 Bild 6
Bild 6
 Bild 7
Bild 7
 Bild 8
Bild 8
 Bild 9
Bild 9
 Bild 10
Y0=1
Bild 10
Y0=1
 Bild 11
Bild 11
 Bild 12
Y1=1
Bild 12
Y1=1
 Bild 13
Y0=1
Bild 13
Y0=1
 Bild 14
Bild 14
 Bild 15
Bild 15
 Bild 16
Y1=1
Bild 16
Y1=1
 Bild 17
Bild 17
 Bild 18
Bild 18
 Bild 19
Bild 19
 Bild 20
Bild 20
 Bild 21
Bild 21
 Bild 22
Y1=1
Bild 22
Y1=1
 Bild 23
Bild 23
 Bild 24
Bild 24
 Bild 25
Bild 25
 Bild 26
Y0=1
Bild 26
Y0=1
 Bild 27
Bild 27
 Bild 28
Bild 28
 Bild 29
Bild 29
 Bild 30
Bild 30
 Bild 31
Y0=1
Bild 31
Y0=1
 Bild 32
Bild 32
 Zum Seitenanfang
Zurück
Home
Zum Seitenanfang
Zurück
Home